福建省龙岩市2018届九年级5月质量检测数学试卷
试卷更新日期:2018-08-28 类型:中考模拟
一、单选题
-
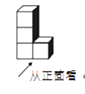
1. 计算 的结果等于( ).A、-2 B、0 C、1 D、22. 下列计算正确的是( ).A、 B、 C、 D、3. 掷两枚质地相同的硬币,正面都朝上的概率是( ).A、1 B、 C、 D、04. 如图是一个由4个相同的正方体组成的立体图形,它的俯视图是( ).
 A、
A、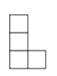 B、
B、 C、
C、 D、
D、 5. 我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,两车空出来;每车坐2人,多出9人无车坐. 问人数和车数各多少?设车 辆,根据题意,可列出的方程是 ( ).A、 B、 C、 D、6. 如图,下列四个条件中,能判断 // 的是( ).
5. 我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,两车空出来;每车坐2人,多出9人无车坐. 问人数和车数各多少?设车 辆,根据题意,可列出的方程是 ( ).A、 B、 C、 D、6. 如图,下列四个条件中,能判断 // 的是( ). A、 B、 C、 D、7. 实数 在数轴上的对应点位置如图所示,把 按照从小到大的顺序排列,正确的是( ).
A、 B、 C、 D、7. 实数 在数轴上的对应点位置如图所示,把 按照从小到大的顺序排列,正确的是( ). A、 B、 C、 D、8. 在同一直角坐标系中,函数 和 的大致图象可能是( ).A、
A、 B、 C、 D、8. 在同一直角坐标系中,函数 和 的大致图象可能是( ).A、 B、
B、 C、
C、 D、
D、 9. 已知 ,则满足 为整数的所有整数 的和是( ).A、-1 B、0 C、1 D、210. 如图, , , ,如果 ,则 的长是( ).
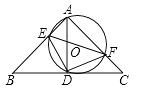
9. 已知 ,则满足 为整数的所有整数 的和是( ).A、-1 B、0 C、1 D、210. 如图, , , ,如果 ,则 的长是( ).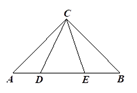 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 使代数式 有意义的 的取值范围是 .12. 2018年春节假期,某市接待游客超3 360 000人次,用科学记数法表示3 360 000,其结果是 .13. 若甲组数据1,2,3,4,5的方差是 ,乙组数据6,7,8,9,10的方差是 ,则
 .(填“
.(填“  ”、“<”或“=”) 14. 如图,在 中, , ,将 绕着点 逆时针旋转到 位置时,点 恰好落在 边上,则在旋转过程中,点 运动到点 的路径长为 .
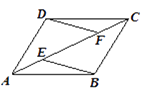
”、“<”或“=”) 14. 如图,在 中, , ,将 绕着点 逆时针旋转到 位置时,点 恰好落在 边上,则在旋转过程中,点 运动到点 的路径长为 . 15. 如图,四边形 和 都是菱形,连接 , ,若 ,则 的面积为 .
15. 如图,四边形 和 都是菱形,连接 , ,若 ,则 的面积为 . 16. 非负数 满足 ,设 的最大值为 ,最小值为 ,则 .
16. 非负数 满足 ,设 的最大值为 ,最小值为 ,则 .三、解答题
-
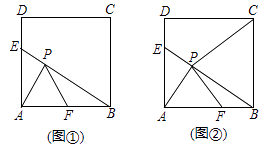
17. 先化简,后求值: ,其中 .18. 如图,在▱ABCD中, 是对角线上的两点,且 ,求证: .
 19. 如图,在每个小正方形的边长为1的网格中, 均为格点.
19. 如图,在每个小正方形的边长为1的网格中, 均为格点. (1)、仅用不带刻度的直尺作 ,垂足为 ,并简要说明道理;(2)、连接 ,求 的周长.20. “不忘初心,牢记使命.”全面建设小康社会到了攻坚克难阶段. 为了解2017年全国居民收支数据国家统计局组织实施了住户收支与生活状况调查,按季度发布.调查采用分层、多阶段、与人口规模大小成比例的概率抽样方法,在全国31个省(区、市)的1650个县(市、区)随机抽选16万个居民家庭作为调查户.已知2017年前三季度居民人均消费可支配收入平均数是2016年前三季度居民人均消费可支配收入平均数的115%,人均消费支出为11423元,根据下列两个统计图回答问题:(以下计算最终结果均保留整数)
(1)、仅用不带刻度的直尺作 ,垂足为 ,并简要说明道理;(2)、连接 ,求 的周长.20. “不忘初心,牢记使命.”全面建设小康社会到了攻坚克难阶段. 为了解2017年全国居民收支数据国家统计局组织实施了住户收支与生活状况调查,按季度发布.调查采用分层、多阶段、与人口规模大小成比例的概率抽样方法,在全国31个省(区、市)的1650个县(市、区)随机抽选16万个居民家庭作为调查户.已知2017年前三季度居民人均消费可支配收入平均数是2016年前三季度居民人均消费可支配收入平均数的115%,人均消费支出为11423元,根据下列两个统计图回答问题:(以下计算最终结果均保留整数) (1)、求年度调查的样本容量及2017年前三季度居民人均消费可支配收入平均数(元);(2)、求在2017年前三季度居民人均消费支出中用于医疗保健所占圆心角度数;
(1)、求年度调查的样本容量及2017年前三季度居民人均消费可支配收入平均数(元);(2)、求在2017年前三季度居民人均消费支出中用于医疗保健所占圆心角度数;
(3)、求在2017年前三季度居民人均消费支出中用于居住的金额.
21. 甲、乙两种笔的单价分别为7元、3元,某学校用78元钱买这两种笔作为数学竞赛一、二等奖奖品,钱恰好用完.若买下的乙种笔是甲种笔的两倍,请问两种笔各买了几支?
22.(1)、知识延伸:如图1,在 中, , ,根据三角函数的定义得: ; (2)、拓展运用:如图2,在锐角三角形 中, .
(2)、拓展运用:如图2,在锐角三角形 中, .①求证: ;
②已知: ,求 的度数.