福建省2018届中考数学模拟试卷（二）

试卷更新日期：2018-08-28 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的绝对值是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、4

查看试题解析
2. PM2.5是指大气中直径不大于0.0000025米的颗粒物，将0.0000025用科学记数法表示为（）

A、2.5×10⁵ B、2.5×10⁶ C、2.5×10^﹣⁵ D、2.5×10^﹣⁶

查看试题解析
3. 计算：（﹣a）⁶÷（﹣a³）等于（）

A、a² B、﹣a² C、a³ D、﹣a³

查看试题解析
4. 如图，所示的几何体的主视图是（）

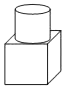A、 B、 C、 D、

查看试题解析
5. 把命题“如果x=y，那么 $\sqrt{x}$ = $\sqrt{y}$ ”作为原命题，对原命题和它的逆命题的真假性的判断，下列说法正确的是（）

A、原命题和逆命题都是真命题 B、原命题和逆命题都是假命题 C、原命题是真命题，逆命题是假命题 D、原命题是假命题，逆命题是真命题

查看试题解析
6. 如图，Rt△ABC中，∠C=90°，AD是∠BAC的平分线，CD=3，AB=10，则△ABD的面积等于（）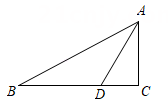

A、30 B、24 C、15 D、10

查看试题解析
7. 已知数据4，4，6，6，8，a的中位数是5，如果这组数据有唯一的众数，那么a的值（）

A、4 B、6 C、8 D、4或6

查看试题解析
8. 如图，AB是⊙O的直径，CD是弦，如果弧AC=弧AD，∠C比∠D大36°，则∠A等于（）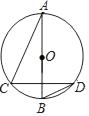

A、24° B、27° C、34° D、37°

查看试题解析
9. 如图，▱ABCD中，对角线AC与AB、AD的夹角分别为α、β，点E是AC上任意一点，给出如下结论：①AB sinα=AD sinβ；②S_△_ABE=S_△_ADE；③ADsinα=AB sinβ．其中正确的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 如果关于x的不等式x＞2a﹣1的最小整数解为x=3，则a的取值范围是（）

A、0＜a＜2 B、a＜2 C、 $\frac{3}{2}$ ≤a＜2 D、a≤2

查看试题解析

二、填空题

11. 已知关于x的方程mx²+2x﹣1=0有两个实数根，则m的取值范围是．

查看试题解析
12. 如图，线段AB的端点A、B分别在x轴和y轴上，且A（2，0），B（0，4），将线段AB绕坐标原点O逆时针旋转90°得线段A'B'，设线段AB'的中点为C，则点C的坐标是．

查看试题解析
13. 已知圆锥的侧面展开图的扇形的弧长为12π，面积为60π，则圆锥的高是．

查看试题解析
14. 一只箱子里有红球和白球各若干个，现从中拿出与白球个数一样多的红球，结果随机摸出一个球是红球的概率为 $\frac{2}{5}$ ，则箱子里原有红球个数与白球个数的比是．

查看试题解析
15. 已知平面直角坐标系xOy中，△OAB为等边三角形，且点A在x轴上，点B在双曲线y= $\frac{2 \sqrt{3}}{x}$ 上，则△OAB的边长是．

查看试题解析

三、解答题

16. 计算：（π﹣4）⁰+（﹣ $\frac{1}{2}$ ）^﹣¹+| $\sqrt{3}$ ﹣2|+tan60°

查看试题解析
17. 化简： $\frac{x^{2}}{x^{2} - 9}$ ÷（ $\frac{1}{x + 3}$ + $\frac{1}{x - 3}$ ）

查看试题解析
18. 如图，在▱ABCD中，AE⊥BD于E，CF⊥BD于F．求证：AE=CF．

查看试题解析
19. 某校为了调查学生书写规范汉字的能力，从七年级1000名学生中随机抽选了部分学生参加测试，并根据测试成绩绘制了如下频数分布表和扇形统计图（尚不完整）
组别
成绩x分
频数（人数）
第1组
x＜60
4
第2组
60≤x＜70
a
第3组
70≤x＜80
20
第4组
80≤x＜90
b
第5组
90≤x＜100
10
请结合图表完成下列各题

(1)、填空：表中a的值为， b的值为，扇形统计图中表示第1组所对应的圆心角度数为．

(2)、若测试成绩不低于80分为优秀，请你估计从该校七年级学生中随机抽查一个学生，他是规范汉字书写优秀的概率是；

(3)、若测试成绩在60～80分之间（含60分，不含80分）为合格，请你估计则该校七年级学生规范汉字书写不合格的人数.

查看试题解析
20. 如图，已知△ABC中，∠C=90°．在BC上求作点D，使AD=BD．当AC=4，CD=3时，求AB的长，（要求尺规作图，保留作图痕迹，不必写作法）

查看试题解析
21. 某商场销售一批进价为10元的新商品，为寻求合适的销售价格，他们进行了4天的试销，试销情况如下表：

第1天
第2天
第3天
第4天
日销售单价x（元）

20
30
40
50
日销售量y（个）

300
200
150
120

(1)、根据试销情况，请你猜测并求出y与x之间的函数关系式；

(2)、若该商场计划每天销售这种商品的利润要达到3600元，问该商品销售单价应定为多少元？

查看试题解析
22. 如图，AB为⊙O的直径，D为⊙O上一点，以AD为斜边作△ADC，使∠C=90°，∠CAD=∠DAB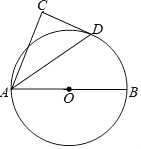

(1)、求证：DC是⊙O的切线；

(2)、若AB=9，AD=6，求DC的长．

查看试题解析
23. 边长为6的等边△ABC中，点P从点A出发沿射线AB方向移动，同时点Q从点B出发，以相同的速度沿射线BC方向移动，连接AQ、CP，直线AQ、CP相交于点D．

(1)、如图①，当点P、Q分别在边AB、BC上时，
①连接PQ，当△BPQ是直角三角形时，AP等于；
②∠CDQ的大小是否随P，Q的运动而变化？如果不会，请求出∠CDQ的度数；如果会，请说明理由；

(2)、当P、Q分别在边AB、BC的延长线上时，在图②中画出点D，并直接写出∠CDQ的度数．

查看试题解析
24. 已知二次函数y=ax²﹣4ax+1

(1)、写出二次函数图象的对称轴：；

(2)、如图，设该函数图象交x轴于点A、B（B在A的右侧），交y轴于点C．直线y=kx+b经过点B、C．
①如果k=﹣ $\frac{1}{3}$ ，求a的值
②设点P在抛物线对称轴上，PC+PB的最小值为 $\sqrt{13}$ ，求点P的坐标．

查看试题解析

组别	成绩x分	频数（人数）
第1组	x＜60	4
第2组	60≤x＜70	a
第3组	70≤x＜80	20
第4组	80≤x＜90	b
第5组	90≤x＜100	10

	第1天	第2天	第3天	第4天
日销售单价x（元）	20	30	40	50
日销售量y（个）	300	200	150	120