北师大版初中数学八年级下学期第一次月考试卷
试卷更新日期:2017-02-24 类型:月考试卷
一、单选题
-
1. 如果不等式 有解,那么m的取值范围是( )
A、m>7 B、m≥7 C、m<7 D、m≤72. 某种品牌奶粉合上标明“蛋白质20%”,它所表达的意思是( )A、蛋白质的含量是20%. B、蛋白质的含量不能是20%. C、蛋白质大含量高于20%. D、蛋白质的含量不低于20%.3.如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的距离是 ( )
 A、3 B、4 C、5 D、64.
A、3 B、4 C、5 D、64.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
 A、3.5 B、4.2 C、5.8 D、75. 若∠AOB=90º,∠BOC=40º,则∠AOB的平分线与∠BOC 的平分线的夹角等于( )A、65º B、25º C、65º或25º D、60º或20º6. 实数a、b在数轴上的位置如图所示,下列各式成立的是( )
A、3.5 B、4.2 C、5.8 D、75. 若∠AOB=90º,∠BOC=40º,则∠AOB的平分线与∠BOC 的平分线的夹角等于( )A、65º B、25º C、65º或25º D、60º或20º6. 实数a、b在数轴上的位置如图所示,下列各式成立的是( )
A、 B、a﹣b>0 C、ab>0 D、a+b>07. 不等式组的解集在数轴上表示为( )
A、 B、
B、 C、
C、 D、
D、 8. 在等腰△ABC中,AB=AC,其周长为16cm,则AB边的取值范围是( )A、1cm<AB<4cm B、3cm<AB<6cm C、4cm<AB<8cm D、5cm<AB<10cm9. 如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是( )
8. 在等腰△ABC中,AB=AC,其周长为16cm,则AB边的取值范围是( )A、1cm<AB<4cm B、3cm<AB<6cm C、4cm<AB<8cm D、5cm<AB<10cm9. 如图,在△ABC中,∠C=90°,AB的垂直平分线交AB与D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是( ) A、13 B、10 C、12 D、510. Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于EF为半径画弧,两弧交于点N,若BC= , 则点M到AC的距离是( )
A、13 B、10 C、12 D、510. Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于EF为半径画弧,两弧交于点N,若BC= , 则点M到AC的距离是( ) A、1 B、 C、 D、311. 在方程组中,若未知数x,y满足x+y>0,则m的取值范围在数轴上的表示应是如图所示的( )A、
A、1 B、 C、 D、311. 在方程组中,若未知数x,y满足x+y>0,则m的取值范围在数轴上的表示应是如图所示的( )A、 B、
B、 C、
C、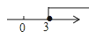 D、
D、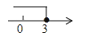 12. 如图,△ABC中,AB=AC,AD是∠BAC的平分线,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
12. 如图,△ABC中,AB=AC,AD是∠BAC的平分线,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( ) A、2对 B、3对 C、4对 D、5对
A、2对 B、3对 C、4对 D、5对二、填空题
-
13. 在△ABC中,AB=AC,AB的中垂线于AC所在的直线相交所得的锐角为40°,则底角∠B的大小为14. 如图,每个小方格都是边长为1的正方形,点A,B是方格纸的两个格点(即正方形的顶点),在这个4X4的方格纸中,找出格点C,使是等腰三角形,这样的点C共有个.
 15. 学习了三角形的有关内容后,张老师请同学们交流这样一个问题:“已知一个等腰三角形的周长是12,其中一条边长为3,求另两条边的长”.同学们经过片刻思考和交流后,小明同学举手讲:“另两条边长为3、6或4.5、4.5”,你认为小明回答是否正确: , 理由是16.
15. 学习了三角形的有关内容后,张老师请同学们交流这样一个问题:“已知一个等腰三角形的周长是12,其中一条边长为3,求另两条边的长”.同学们经过片刻思考和交流后,小明同学举手讲:“另两条边长为3、6或4.5、4.5”,你认为小明回答是否正确: , 理由是16.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= cm.
 17. 如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为
17. 如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为 18. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是
18. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是
三、计算题
-
19. 解下列不等式组,并把解集在数轴上表示出来.
四、解答题
-
20. 解一元一次不等式组 , 并把解在数轴上表示出来.
 21. 为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍?22. 已知和都是关于x、y的方程y=kx+b的解.(1)、求k、b的值(2)、若不等式3+2x>m+3x的最大整数解是k,求m的取值范围.23. 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
21. 为了举行班级晚会,孔明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,且买的球拍尽可能多,那么孔明应该买多少个球拍?22. 已知和都是关于x、y的方程y=kx+b的解.(1)、求k、b的值(2)、若不等式3+2x>m+3x的最大整数解是k,求m的取值范围.23. 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长. 24. 瑶海教育局计划在3月12日植树节当天安排A,B两校部分学生到郊区公园参加植树活动.已知A校区的每位学生往返车费是6元,B校每位学生的往返车费是10元,要求两所学校均要有学生参加,且A校参加活动的学生比B校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求A,B两校最多各有多少学生参加?25. (1)如图1,Rt△ABC中,∠ACB=90°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
24. 瑶海教育局计划在3月12日植树节当天安排A,B两校部分学生到郊区公园参加植树活动.已知A校区的每位学生往返车费是6元,B校每位学生的往返车费是10元,要求两所学校均要有学生参加,且A校参加活动的学生比B校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求A,B两校最多各有多少学生参加?25. (1)如图1,Rt△ABC中,∠ACB=90°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;(2)如图2,在△ABC中,∠ACB=40°,点D、E在直线AB上,且AD=AC,BE=BC,则∠DCE的度数;
(3)在△ABC中,∠ACB=n°(0<n<180°),点D、E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).
 26. 自学下面材料后,解答问题.
26. 自学下面材料后,解答问题.分母中含有未知数的不等式叫分式不等式.如:等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则>0;若a<0,b<0,则>0;
(2)若a>0,b<0,则<0;若a<0,b>0,则<0.
反之:(1)若>0,则或
(2)<0,则____________ .
根据上述规律,求不等式>0的解集.
-