人教版初中数学八年级下学期第一次月考试卷

试卷更新日期：2017-02-24 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式中，正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $- \sqrt{3^{2}} = - 3$ C、 $\sqrt{{(\pm 3)}^{2}} = \pm 3$ D、 $\sqrt{3^{2}} = \pm 3$

查看试题解析
2. 下列二次根式中，与 $\sqrt{24}$ 是同类二次根式的是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析
3.
如图，a∥b，下列线段中是a，b之间的距离的是（　　）

A、AB B、AE C、EF D、BC

查看试题解析
4. 下列说法正确的是（）

A、等腰梯形的对角线互相平分． B、一组对边平行，另一组对边相等的四边形是平行四边形． C、线段的垂直平分线上的点到线段两个端点的距离相等． D、两边对应成比例且有一个角对应相等的两个三角形相似．

查看试题解析
5.
如图，把长方形ABCD沿EF对折，若∠1=50⁰ ，则∠AEF的度数等于（）

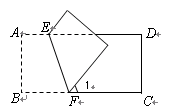A、25º B、50º C、100º D、115º

查看试题解析
6. 满足下列条件的△ABC中，不是直角三角形的是（）

A、∠A＝∠B－∠C B、∠A︰∠B︰∠C＝1︰1︰2 C、a︰b︰c＝1︰1︰2 D、b²＝c²－a²

查看试题解析
7. 若 $\sqrt{{(a - 2)}^{2}} = 2 - a$ ，则a的取值范围是（　　）

A、a=2 B、a＞2 C、a≥2　　　　 D、a≤2

查看试题解析
8.
如图所示有一块直角三角形纸片，两直角边分别为：AC =6cm，BC = 8 cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）

A、2 cm B、3 cm C、4 cm D、5 cm

查看试题解析
9.
如图为一个平行四边形ABCD，其中H、G两点分别在BC、CD上，AH⊥BC，AG⊥CD，且AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4四个角．若AH=5，AG=6，则下列关系何者正确（　　）

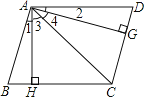A、∠1=∠2 B、∠3=∠4 C、BH=GD D、HC=CG

查看试题解析
10.
圆柱形纸筒沿母线AB剪开铺平，得到一个矩形（如图）．如果将这个纸筒沿线路B⇒M⇒A剪开铺平，得到的图形是（　　）

A、矩形 B、半圆 C、三角形 D、平行四边形

查看试题解析
11. 如图，在平行四边形ABCD中，CE⊥AB且E为垂足．如果∠A=125°，则∠BCE=（）

A、55° B、35° C、25° D、30°

查看试题解析
12.
在矩形ABCD中放入六个长、宽都相同的小长方形，所标尺寸如图所示，求小长方形的宽AE．若AE=x（cm），依题意可得方程（　　）

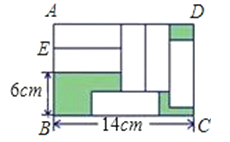A、6+2x=14﹣3x B、6+2x=x+（14﹣3x） C、14﹣3x=6 D、6+2x=14﹣x

查看试题解析

二、填空题

13. 计算：2 $\sqrt{2}$ ﹣ $\sqrt{32}$ = ．

查看试题解析
14. 比较大小：4 $\sqrt{15}$ （填“＞”或“＜”）

查看试题解析
15. 两条平行线间的所有线段都相等．

查看试题解析
16. 已知a、b满足 $\sqrt{a - 2014}$ + $\sqrt{2014 - a}$ =b，则a+b的值为．

查看试题解析
17. 已知一个直角三角形的两条直角边的差为2，两条直角边的平方和为8，则这个直角三角形的面积是

查看试题解析
18. 已知直线a∥b，点M到直线a的距离是5cm，到直线b的距离是3cm，那么直线a和直线b之间的距离为

查看试题解析

三、计算题

19. 计算：（ $\frac{\sqrt{2}}{\sqrt{3}} - \sqrt{6}$ ） $\div \sqrt{3}$ ．

查看试题解析

四、解答题

20.
如图，已知，l₁∥l₂ ， C₁在l₁上，并且C₁A⊥l₂ ， A为垂足，C₂ ， C₃是l₁上任意两点，点B在l₂上．设△ABC₁的面积为S₁ ， △ABC₂的面积为S₂ ， △ABC₃的面积为S₃ ，小颖认为S₁=S₂=S₃ ，请帮小颖说明理由

查看试题解析
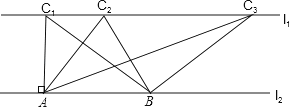21.
如图，梯形ABCD是由三个直角三角形拼成的，各直角边的长度如图所示。
(1)请你运用两种方法计算梯形ABCD的面积；
(2)根据（1）的计算，探索a，b，c三者之间的关系，并用式子表示出来。

查看试题解析
22.
如图，一块草地的中间有一条宽度不变的弯路，AC∥BD，CE∥EF，请给出一种方案，把道路改直，且草地的种植面积保持不变．

查看试题解析
23.
如图，直线l₁∥l₂ ， l₁和AB的夹角∠DAB=135°，且AB=50mm，求两平行线l₁和l₂之间的距离．

查看试题解析
24.
我们运用图（Ⅰ）中大正方形的面积可表示为（a+b）² ，也可表示为c³+4（ $\frac{1}{2}$ ab），即（a+b）²=c²+4（ $\frac{1}{2}$ ab）由此推导出一个重要的结论a²+b²=c² ，这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．
（1）请你用图（Ⅱ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．
（2）请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+2y）²=x²+4xy+4y² ．

查看试题解析