北师大版初中数学七年级下学期第一次月考试卷
试卷更新日期：2017-02-24 类型：月考试卷
一、单选题
-
1. 小王在下面的计算中只做对了一道题，他做对的题目是（ ）A、3a7•2a6=6a42 B、（a7）6=a42 C、a42÷a7=a6 D、a6+a6=a122.
如图L1∥L2 ， ∠1=120°，∠2=100°，则∠3 =（ ）
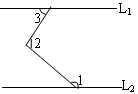A、20° B、40° C、50° D、60°3. 下列多项式乘法中，可用平方差公式计算的是（ ）A、（2a+b）（2a﹣3b） B、（x+1）（1+x） C、（x﹣2y）（x+2y） D、（﹣x﹣y）（x+y）4. 设m＞n＞0，m2＋n2＝4mn，则＝
A、 B、 C、2 D、35. 如图所示，与∠α构成同位角的角的个数为( )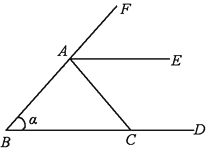
A、1 B、2 C、3 D、46.如图，某同学在课桌上随意将一块三角板的直角叠放在直尺上，则∠1+∠2的度数是（ ）
A、45° B、60° C、90° D、180°7. 李老师做了个长方形教具，其中一边长为2a+b，另一边长为a﹣b，则该长方形的面积为（ ）A、6a+b B、2a2﹣ab﹣b2 C、3a D、10a﹣b8.一条船在灯塔的北偏东30°方向，那么灯塔在船的什么方向（ ）
A、南偏西30° B、西偏南40° C、南偏西60° D、北偏东30°
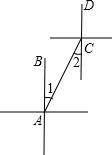
9.如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（ ）
A、75° B、55° C、40° D、35°10. 如图，把边长为（a+2）的正方形纸片剪出一个边长为a的正方形之后，剩余部分又剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为2，则长方形的面积是（ ）
A、2（2a+2） B、2a+4 C、4a+8 D、2（a+4）11.如图，已知AB∥CD，若∠A=25°，∠E=40°，则∠C等于（ ）
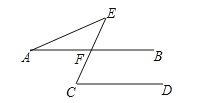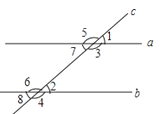
A、40° B、65° C、115° D、25°12.如图，直线a、b都与直线c相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠4+∠7=180°；④∠5+∠8=180°．其中能判断a∥b的条件是（ ）
A、①③ B、②④ C、①③④ D、①②③④二、填空题
-
13. 若2m=4，2n=8，则2m+n=。
14.图中是对顶角量角器，用它测量角的原理是 ．
15. 如果a2n﹣1•an+5=a16 ， 那么n=（n是整数）．
16. 如图所示，与∠C构成同旁内角的有个．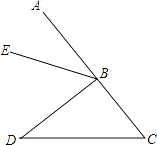
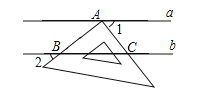
17.如图，直线a∥b，三角板的直角顶点A落在直线a上，两条直线分别交直线b于B、C两点．若∠1=42°，则∠2的度数是 ．
18. 如图所示：直线AB与CD相交于O，已知∠1=30°，OE是∠BOC的平分线，则∠2=°，∠3=°．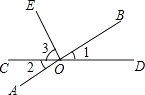
三、计算题
-
19. 已知a-b=3，ab=2，求：
（1）(a＋b)2 ，
（2）a2-6ab＋b2的值．
20. 先化简，再求值：[（xy+2）（xy－2）－2（x2y2－2）]÷（xy），其中x=10，y=－ ．
21. 宇宙空间的年龄通常以光年作单位，1光年是光在一年内通过的距离，如果光的速度为每秒3×107千米，一年约为3.2×107秒，那么1光年约为多少千米？
四、作图题
-
22.
作图题：（只保留作图痕迹）如图，在方格纸中，有两条线段AB、BC．
利用方格纸完成以下操作：
（1）过点A作BC的平行线；
（2）过点C作AB的平行线，与（1）中的平行线交于点D；
（3）过点B作AB的垂线．
五、解答题
-
23.
如图，∠1=∠C，AC平分∠DAB，求证：DC∥AB．
24.图a是一个长为2 m、宽为2 n的长方形， 沿图中虚线用剪刀均分成四块小长方形， 然后按图b的形状拼成一个正方形.
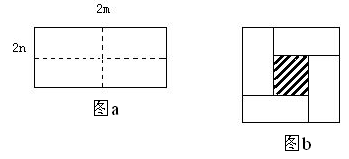
(1) 写出图b中的阴影部分的正方形的边长；
(2) 写出图b中阴影部分的面积：
(3)观察图b写出下列三个代数式(m+n)²，(m-n)²，mn之间的等量关系；(4)根据（3）题中的等量关系，解决如下问题：若a+b=7，ab=5 ， 求(a-b)²
25.用四块完全相同的小长方形拼成的一个“回形”正方形．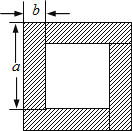
(1)、用不同代数式表示图中的阴影部分的面积，你能得到怎样的等式，试用乘法公式说明这个等式成立；(2)、利用（1）中的结论计算：a+b=2，ab= ， 求a﹣b；(3)、根据（1）中的结论，直接写出x+和x﹣之间的关系；若x2﹣3x+1=0，分别求出x+和（x﹣）2的值．26.如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，当∠E=90°且AB与CD的位置关系保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD否存在确定的数量关系？并说明理由；
（3）如图3，P为线段AC上一定点，点Q为直线CD上一动点且AB与CD的位置关系保持不变，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．
-