2017年安徽省淮北市高考数学一模试卷（理科）

试卷更新日期：2017-02-24 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合P=（﹣∞，0]∪（3，+∞），Q={0，1，2，3}，则（∁_RP）∩Q=（）

A、{0，1} B、{0，1，2} C、{1，2，3} D、{x|0≤x＜3}

查看试题解析
2. 复数 $z = \frac{i}{1 - i}$ 的共轭复数的模为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、1 D、2

查看试题解析
3. 已知x，y满足线性约束条件 ${\begin{matrix} y - x \leq 3 \\ \begin{array}{l} x + y \leq 5 \\ y \geq λ \end{array} \end{matrix}$ ，若z=x+4y的最大值与最小值之差为5，则实数λ的值为（）

A、3 B、 $\frac{7}{3}$ C、 $\frac{3}{2}$ D、1

查看试题解析
4. 函数f（x）=|x|+ $\frac{a}{x}$ （其中a∈R）的图像不可能是（）

A、 B、 C、 D、

查看试题解析
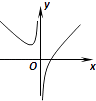5. 已知三个数1，a，9成等比数列，则圆锥曲线 $\frac{x^{2}}{a} + \frac{y^{2}}{2} = 1$ 的离心率为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{5}$ C、 $\sqrt{5}$ 或 $\frac{\sqrt{10}}{2}$ D、 $\frac{\sqrt{3}}{3}$ 或 $\frac{\sqrt{10}}{2}$

查看试题解析
6. 在△ABC中， $∠ A = \frac{π}{3} ， B C = 4 \sqrt{3}$ ，则△ABC的周长为（）

A、 $4 \sqrt{3} + 8 \sqrt{3} \sin (B + \frac{π}{6})$ B、 $4 \sqrt{3} + 8 \sin (B + \frac{π}{3})$ C、 $4 \sqrt{3} + 8 \sqrt{3} \cos (B + \frac{π}{6})$ D、 $4 \sqrt{3} + 8 \cos (B + \frac{π}{3})$

查看试题解析
7. 下列说法正确的是（）
（1．）已知等比数列{a_n}，则“数列{a_n}单调递增”是“数列{a_n}的公比q＞1”的充分不必要条件；
（2．）二项式 ${(2 x + \frac{1}{\sqrt{x}})}^{5}$ 的展开式按一定次序排列，则无理项互不相邻的概率是 $\frac{1}{5}$ ；
（3．）已知 $S = \int_{0}^{\frac{1}{2}} \sqrt{\frac{1}{4} - x^{2}} d x$ ，则 $S = \frac{π}{16}$ ；
（4．）为了解1000名学生的学习情况，采用系统抽样的方法，从中抽取容量为40的样本，则分段的间隔为40．

A、（1）（2） B、（2）（3） C、（1）（3） D、（2）（4）

查看试题解析
8. 执行如图的程序框图，则输出S的值为（）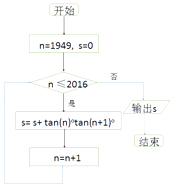

A、 $\frac{\tan 2017^{0} - \tan 1949^{0}}{\tan 1^{0}}$ ﹣67 B、 $\frac{\tan 2016^{0} - \tan 1949^{0}}{\tan 1^{0}}$ ﹣67 C、 $\frac{\tan 2017^{0} - \tan 1949^{0}}{\tan 1^{0}}$ ﹣68 D、 $\frac{\tan 2016^{0} - \tan 1949^{0}}{\tan 1^{0}}$ ﹣68

查看试题解析
9. 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形，则该几何体的体积（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
10. 若函数f（x）在其图像上存在不同的两点A（x₁ ， y₁），B（x₂ ， y₂），其坐标满足条件：|x₁x₂+y₁y₂|﹣ $\sqrt{x_{1}^{2} + y_{1}^{2}} \cdot \sqrt{x_{2}^{2} + y_{2}^{2}}$ 的最大值为0，则称f（x）为“柯西函数”，
则下列函数：
①f（x）=x+ $\frac{1}{x}$ （x＞0）；
②f（x）=lnx（0＜x＜3）；
③f（x）=2sinx；
④f（x）= $\sqrt{2 x^{2} - 8}$ ．
其中为“柯西函数”的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 已知直线l₁与圆心为C的圆（x﹣1）²+（y﹣2）²=4相交于不同的A，B两点，对平面内任意点Q都有 $\vec{Q C} = λ \vec{Q A} + (1 - λ) \vec{Q B}$ ，λ∈R，又点P为直线l₂：3x+4y+4=0上的动点，则 $\vec{P A} \cdot \vec{P B}$ 的最小值为（）

A、21 B、9 C、5 D、0

查看试题解析
12. 已知定义在（0，+∞）的函数f（x），其导函数为f′（x），满足：f（x）＞0且 $\frac{2 x + 3}{x} > - \frac{f^{'} (x)}{f (x)}$ 总成立，则下列不等式成立的是（）

A、e^2e⁺³f（e）＜e^2ππ³f（π） B、e^2e⁺³f（π）＞e^2ππ³f（e） C、e^2e⁺³f（π）＜e^2ππ³f（e） D、e^2e⁺³f（e）＞e^2ππ³f（π）

查看试题解析

二、填空题

13. 已知实数a，b均大于0，且 $(\frac{1}{a} + \frac{1}{b}) \sqrt{a^{2} + b^{2}} \geq 2 m - 4$ 总成立，则实数m的取值范围是．

查看试题解析
14. 设随机变量ξ服从正态分布N（2，9），若P（ξ＞c+1）=P（ξ＜c﹣1），则c= ．

查看试题解析
15. 函数 $f (x) = 2 \sin x + 2 \cos x - \sin 2 x + 1 ， x \in [- \frac{5 π}{12} ， \frac{π}{3})$ 的值域是．

查看试题解析
16. 等差数列{a_n}的前n项和为S_n ，数列{b_n}是等比数列，且满足a₁=3，b₁=1，b₂+S₂=10，a₅﹣2b₂=a₃ ，数列{ $\frac{a_{n}}{b_{n}}$ }的前n项和T_n ，若T_n＜M对一切正整数n都成立，则M的最小值为．

查看试题解析

三、解答题

17. 在△ABC中，设边a，b，c所对的角为A，B，C，且A，B，C都不是直角，（bc﹣8）cosA+accosB=a²﹣b² ．
（Ⅰ）若b+c=5，求b，c的值；
（Ⅱ）若 $a = \sqrt{5}$ ，求△ABC面积的最大值．

查看试题解析
18. 为调查了解某省属师范大学师范类毕业生参加工作后，从事的工作与教育是否有关的情况，该校随机调查了该校80位性别不同的2016年师范类毕业大学生，得到具体数据如表：
与教育有关
与教育无关
合计
男
30
10
40
女
35
5
40
合计
65
15
80

(1)、能否在犯错误的概率不超过5%的前提下，认为“师范类毕业生从事与教育有关的工作与性别有关”？
参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ （n=a+b+c+d）．
附表：
P（K²≥k₀）
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
k₀
0.455
0.708
1.323
2.072
2.706
3.841
5.023
6.635

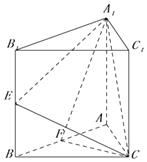
(2)、求这80位师范类毕业生从事与教育有关工作的频率；

(3)、以（2）中的频率作为概率．该校近几年毕业的2000名师范类大学生中随机选取4名，记这4名毕业生从事与教育有关的人数为X，求X的数学期望E（X）．

查看试题解析
19. 正三棱柱ABC﹣A₁B₁C₁底边长为2，E，F分别为BB₁ ， AB的中点．
（I）已知M为线段B₁A₁上的点，且B₁A₁=4B₁M，求证：EM∥面A₁FC；
（II）若二面角E﹣A₁C﹣F所成角的余弦值为 $\frac{2 \sqrt{7}}{7}$ ，求AA₁的值．

查看试题解析
20. 已知椭圆C₁： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率e= $\frac{\sqrt{3}}{2}$ ，且过点 $(2 ， \sqrt{3})$ ，直线l₁：y=kx+m（m＞0）与圆C₂：（x﹣1）²+y²=1相切且与椭圆C₁交于A，B两点．
（Ⅰ）求椭圆C₁的方程；
（Ⅱ）过原点O作l₁的平行线l₂交椭圆于C，D两点，设|AB|=λ|CD|，求λ的最小值．

查看试题解析
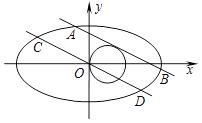21. 已知函数发f（x）=（x+1）lnx﹣ax+2．

(1)、当a=1时，求在x=1处的切线方程；

(2)、若函数f（x）在定义域上具有单调性，求实数a的取值范围；

(3)、求证： $\frac{1}{3} + \frac{1}{5} + \frac{1}{7} + \dots + \frac{1}{2 n + 1} < \frac{1}{2} \ln (n + 1)$ ，n∈N^* ．

查看试题解析

四、选做题

22. 以平面直角坐标系的原点为极点，以x轴的正半轴为极轴建立极坐标系．设曲线C的参数方程为 ${\begin{matrix} x = 2 \cos α \\ y = \sqrt{3} \sin α \end{matrix}$ （α是参数），直线l的极坐标方程为ρcos（θ+ $\frac{π}{6}$ ）=2 $\sqrt{3}$ ．

(1)、求直线l的直角坐标方程和曲线C的普通方程；

(2)、设点P为曲线C上任意一点，求点P到直线l的距离的最大值．

查看试题解析
23. 已知函数f（x）=|x+a|+|x﹣2|

(1)、当a=﹣3时，求不等式f（x）≥3的解集；

(2)、若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．

查看试题解析

	与教育有关	与教育无关	合计
男	30	10	40
女	35	5	40
合计	65	15	80

P（K²≥k₀）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010
k₀	0.455	0.708	1.323	2.072	2.706	3.841	5.023	6.635