2016年甘肃省平凉市静宁县高考数学一模试卷（理科）

试卷更新日期：2017-02-24 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合M={x| $\frac{x}{x - 1}$ ≥0，x∈R}，N={y|y=3x²+1，x∈R}，则M∩N为（）

A、{x|x＞1} B、{x|x≥1} C、{x＞1或x≤0} D、{x|0≤x≤1}

查看试题解析
2. 已知i为虚数单位，图中复平面内的点A表示复数z，则表示复数 $\frac{z}{1 + i}$ 的点是（）

A、M B、N C、P D、Q

查看试题解析
3. 已知命题P：有的三角形是等边三角形，则（）

A、¬P：有的三角形不是等边三角形 B、¬P：有的三角形是不等边三角形 C、¬P：所有的三角形都是等边三角形 D、¬P：所有的三角形都不是等边三角形

查看试题解析
4. 在△ABC中， $\vec{A B}$ • $\vec{B C}$ ＞0，则该三角形的形状是（）

A、钝角三角形 B、锐角三角形 C、直角三角形 D、不能确定

查看试题解析
5. 如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则 $\vec{A F} - \vec{D B}$ =（）

A、 $\vec{F D}$ B、 $\vec{F C}$ C、 $\vec{F E}$ D、 $\vec{B E}$

查看试题解析
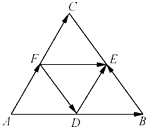6. 函数y=sin（ $\frac{π}{4}$ ﹣2x）的单调增区间是（）

A、 $[k π - \frac{3 π}{8}$ ， $k π + \frac{3 π}{8}$ ]（k∈z） B、 $[k π + \frac{π}{8}$ ， $k π + \frac{5 π}{8}$ ]（k∈z） C、 $[k π - \frac{π}{8}$ ， $k π + \frac{3 π}{8}$ ]（k∈z） D、 $[k π + \frac{3 π}{8}$ ， $k π + \frac{7 π}{8}$ ]（k∈z）

查看试题解析
7. 直线y=x﹣4与曲线y= $\sqrt{2 x}$ 及x轴所围成图形的面积是（）

A、 $\frac{64}{3}$ B、 $\frac{40}{3}$ C、 $\frac{56}{3}$ D、 $\frac{38}{3}$

查看试题解析
8. 已知某个几何体的三视图如图（主视图的弧线是半圆），根据图中标出的数据，这个几何体的体积是（）

A、288+36π B、60π C、288+72π D、288+18π

查看试题解析
9. 设等差数列 {a_n}的前n项和为S_n ，若S₁₂=288，S₉=162，则S₆=（）

A、18 B、36 C、54 D、72

查看试题解析
10. 若过点A（4，0）的直线l与曲线（x﹣2）²+y²=1有公共点，则直线l的斜率的取值范围为（）

A、 $[- \sqrt{3} ， \sqrt{3}]$ B、 $(- \sqrt{3} ， \sqrt{3})$ C、 $[- \frac{\sqrt{3}}{3} ， \frac{\sqrt{3}}{3}]$ D、 $(- \frac{\sqrt{3}}{3} ， \frac{\sqrt{3}}{3})$

查看试题解析
11. △ABC各角的对应边分别为a，b，c，满足 $\frac{b}{a + c}$ + $\frac{c}{a + b}$ ≥1，则角A的范围是（）

A、（0， $\frac{π}{3}$ ] B、（0， $\frac{π}{6}$ ] C、[ $\frac{π}{3}$ ，π） D、[ $\frac{π}{6}$ ，π）

查看试题解析
12. 已知函数f（x）=e^x﹣1，g（x）=﹣x²+4x﹣3，若有f（a）=g（b），则b的取值范围为（）

A、 $[2 - \sqrt{2} ， 2 + \sqrt{2}]$ B、（2﹣ $\sqrt{2}$ ，2+ $\sqrt{2}$ ） C、[1，3] D、（1，3）

查看试题解析

二、填空题

13. 若f（x）=3x+sinx，则满足不等式f（2m﹣1）+f（3﹣m）＞0的m的取值范围为．

查看试题解析
14. 在数列{a_n}中，已知a₁=1，a_n₊₁﹣a_n=sin $\frac{(n + 1) π}{2}$ ，记S_n为数列{a_n}的前n项和，则S₂₀₁₅= ．

查看试题解析
15. 已知x，y满足 ${\begin{matrix} y - 2 \leq 0 \\ x + 3 \geq 0 \\ x - y - 1 \leq 0 \end{matrix}$ 则 $\frac{x + 2 y - 6}{x - 4}$ 的取值范围是．

查看试题解析
16. 已知函数f（x）= ${\begin{matrix} | \lg (- x) | ， x < 0 \\ x^{2} - 6 x + 4 ， x \geq 0 \end{matrix}$ ，若关于x的方程f²（x）﹣bf（x）+1=0有8个不同根，则实数b的取值范围是．

查看试题解析

三、解答题

17. 已知p：|1﹣ $\frac{x - 1}{3}$ |≤2，q：（x﹣1+m）（x﹣1﹣m）＜0（m＞0）且q是p的必要不充分条件，求实数m的取值范围．

查看试题解析
18. 已知数列{a_n}满足：S_n=1﹣a_n（n∈N^*），其中S_n为数列{a_n}的前n项和．
（Ⅰ）试求{a_n}的通项公式；
（Ⅱ）若数列{b_n}满足： $b_{n} = \frac{n}{a_{n}}$ （n∈N^*），试求{b_n}的前n项和公式T_n ．

查看试题解析
19. 在△ABC中，角A，B，C所对的边分别为a，b，c，若1+ $\frac{\tan A}{\tan B}$ = $\frac{2 c}{b}$ ．

(1)、求角A的大小；

(2)、若函数f（x）=2sin²（x+ $\frac{π}{4}$ ）﹣ $\sqrt{3}$ cos2x，x∈[ $\frac{π}{4}$ ， $\frac{π}{2}$ ]，在x=B处取到最大值a，求△ABC的面积．

查看试题解析
20. 如图，四棱锥P﹣ABCD中，ABCD为矩形，△PAD为等腰直角三角形，∠APD=90°，面PAD⊥面ABCD，且AB=1，AD=2，E、F分别为PC和BD的中点．

(1)、证明：EF∥面PAD；

(2)、证明：面PDC⊥面PAD；

(3)、求锐二面角B﹣PD﹣C的余弦值．

查看试题解析
21. 椭圆H： $\frac{x^{2}}{a^{2}}$ +y²=1（a＞1），原点O到直线MN的距离为 $\frac{\sqrt{3}}{2}$ ，其中点M（0，﹣1），点N（a，0）．

(1)、求该椭圆H的离心率e；

(2)、经过椭圆右焦点F₂的直线l和该椭圆交于A，B两点，点C在椭圆上，O为原点，
若 $\vec{O C}$ = $\frac{1}{2} \vec{O A}$ + $\frac{\sqrt{3}}{2}$ $\vec{O B}$ ，求直线l的方程．

查看试题解析
22. 已知f（x）=xlnx，g（x）=x³+ax²﹣x+2

(1)、求函数f（x）的单调区间；

(2)、求函数f（x）在[t，t+2]（t＞0）上的最小值；

(3)、对一切的x，2f（x）≤g′（x）+2恒成立，求实数a的取值范围．

查看试题解析