2015-2016学年河北省唐山市滦县八年级下学期期中数学试卷

试卷更新日期：2017-02-24 类型：期中考试

进入出卷网下载

一、选择题

1. 为了了解某县八年级学生的体重情况从中抽取了200名学生进行体重测试．在这个问题中，下列说法错误的是（）

A、200学生的体重是总体 B、200学生的体重是一个样本 C、每个学生的体重是个体 D、全县八年级学生的体重是总体

查看试题解析
2. 点M（1﹣m，3﹣m）在x轴上，则点M坐标为（）

A、（0，﹣4） B、（4，0） C、（﹣2，0） D、（0，﹣2）

查看试题解析
3. 如图是在方格纸上画出的小旗图案，若用（0，0）表示A点，（0，4）表示B点，那么C点的位置可表示为（）

A、（0，3） B、（2，3） C、（3，2） D、（3，0）

查看试题解析
4. 一支蜡烛长20厘米，点燃后每小时燃烧5厘米，燃烧时剩下的高度h（厘米）与燃烧时间t（时）的函数关系的图像是（）

A、 B、 C、 D、

查看试题解析
5. 在平面直角坐标系中，一个图案上各个点的横坐标和纵坐标分别加正数a，则所得的图案与原来图案相比（　　）

A、形状不变，大小扩大到原来的a倍 B、图案向右平移了a个单位 C、图案向上平移了a个单位 D、图案向右平移了a个单位，并且向上平移了a个单位

查看试题解析
6. 已知点P的坐标（2a，6﹣a），且点P到两坐标轴的距离相等，则点P的坐标是（）

A、（12，﹣12）或（4，﹣4） B、（﹣12，12）或（4，4） C、（﹣12，12） D、（4，4）

查看试题解析
7. 下列正确结论的个数是（）
①平行四边形内角和为360°；②平行四边形对角线相等；③平行四边形对角线互相平分；④平行四边形邻角互补．

A、1 B、2 C、3 D、4

查看试题解析
8. 下列图形中，表示一次函数y=mx+n与正比例函数y=mnx（m，n为常数，且mn≠0）的图像的是（）

A、 B、 C、 D、

查看试题解析
9. 根据表中一次函数的自变量x与函数y的对应值，可得p的值为（）
x
﹣2
0
1
y
3
p
0

A、1 B、﹣1 C、3 D、﹣3

查看试题解析
10.
如图所示的计算程序中，y与x之间的函数关系所对应的图像应为（）

A、 B、 C、 D、

查看试题解析
11. 小高从家门口骑车去单位上班，先走平路到达点A，再走上坡路到达点B，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是（）

A、12分钟 B、15分钟 C、25分钟 D、27分钟

查看试题解析
12. 如图，点A的坐标为（﹣1，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为（）

A、（0，0） B、（ $\frac{\sqrt{2}}{2}$ ，﹣ $\frac{\sqrt{2}}{2}$ ） C、（﹣ $\frac{1}{2}$ ，﹣ $\frac{1}{2}$ ） D、（﹣ $\frac{\sqrt{2}}{2}$ ，﹣ $\frac{\sqrt{2}}{2}$ ）

查看试题解析
13. 如图所示，▱ABCD的对角线AC，BD相交于点O，AE=EB，OE=3，AB=5，▱ABCD的周长（）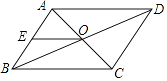

A、11 B、13 C、16 D、22

查看试题解析
14. 如图，直线y=kx+b经过点A（﹣1，﹣2）和点B（﹣2，0），直线y=2x过点A，则不等式2x＜kx+b＜0的解集为（）

A、x＜﹣2 B、﹣2＜x＜﹣1 C、﹣2＜x＜0 D、﹣1＜x＜0

查看试题解析
15.
如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（）

A、N处 B、P处 C、Q处 D、M处

查看试题解析
16. 如图，直线l：y=﹣ $\frac{2}{3}$ x﹣3与直线y=a（a为常数）的交点在第四象限，则a可能在（）

A、1＜a＜2 B、﹣2＜a＜0 C、﹣3≤a≤﹣2 D、﹣10＜a＜﹣4

查看试题解析

二、填空题

17. 在函数 $y = \frac{1}{\sqrt{x + 2}}$ 的表达式中，自变量x取值范围是．

查看试题解析
18. 已知点A（﹣1，a），B（2，b）在函数y=﹣3x+4的图像上，则a与b的大小关系是．

查看试题解析
19. 如图，等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm，AC与MN在同一直线上，开始时A点与M点重合，让向右运动，最后A点与N点重合，则重叠部分面积ycm²与MA长度xcm之间关系式；自变量的取值范围是．

查看试题解析
20. 如图，在直角坐标系中，已知点A（﹣3，0），B（0，4），对△OAB连续作旋转变换，依次得到三角形1、2、3、4…．则三角形2016的直角顶点坐标为．

查看试题解析

三、解答题

21. 某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市24000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：
分数段
频数
频率
x＜60
20
0.10
60≤x＜70
28
0.14
70≤x＜80
54
0.27
80≤x＜90
a
0.20
90≤x＜100
24
0.12
100≤x＜110
18
b
110≤x＜120
16
0.08
请根据以上图表提供的信息，解答下列问题：

(1)、表中a和b所表示的数分别为：a= ， b=；

(2)、请在图中，补全频数分布直方图；

(3)、如果把成绩在90分以上（含90分）定为优秀，那么该市24000名九年级考生数学成绩为优秀的学生约有多少名？

查看试题解析
22. 如图所示，在△ABC中，点A的坐标为（0，1），点C的坐标为（4，3），

(1)、点A关于x轴的对称点的坐标；

(2)、点C关于y轴的对称点的坐标；

(3)、如果要使△ABD与△ABC全等，那么点D的坐标是．

查看试题解析
23. 在平面坐标系中△ABO位置如图，已知OA=AB=5，OB=6，

(1)、求A、B两点的坐标．

(2)、点Q为y轴上任意一点，直接写出满足：S_△_ABO=S_△_AOQ的Q点坐标．

查看试题解析
24. △ABC的中线BD、CE相交于O，F，G分别是BO、CO的中点，求证：EF∥DG，且EF=DG．

查看试题解析
25. 甲乙两人同时登西山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图像所提供的信息解答下列问题：

(1)、甲登山的速度是每分钟米，乙在A地提速时距地面的高度b为米．

(2)、若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度y（米）与登山时间x（分）之间的函数关系式．

(3)、登山多长时间时，乙追上了甲此时乙距A地的高度为多少米？

查看试题解析
26. 无锡阳山地区有A、B两村盛产水蜜桃，现A村有水蜜桃200吨，B村有水蜜桃300吨．计划将这些水蜜桃运到C、D两个冷藏仓库，已知C仓库可储存240吨，D仓库可储存260吨；从A村运往C、D两处的费用分别为每吨20元和25元，从B村运往C，D两处的费用分别为每吨15元和18元．设从A村运往C仓库的水蜜桃重量为x吨，A、B两村运往两仓库的水蜜桃运输费用分别为y_A元和y_B元．

(1)、请先填写下表，
收地运地
C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
再根据所填写内容分别求出y_A、y_B与x之间的函数关系式；
y_A：；y_B：

(2)、试讨论A、B两村中，哪个村的运费较少；

(3)、考虑到B村的经济承受能力，B村的水蜜桃运费不得超过4830元．在这种情况下，请问怎样调运，才能使两村运费之和最小？求出这个最小值．

查看试题解析

分数段	频数	频率
x＜60	20	0.10
60≤x＜70	28	0.14
70≤x＜80	54	0.27
80≤x＜90	a	0.20
90≤x＜100	24	0.12
100≤x＜110	18	b
110≤x＜120	16	0.08

收地运地	C	D	总计
A	x吨		200吨
B			300吨
总计	240吨	260吨	500吨

x	﹣2	0	1
y	3	p	0