2018-2019学年数学北师大版八年级上册第二章《实数》单元测试卷

试卷更新日期：2018-08-23 类型：单元试卷

进入出卷网下载

一、选择题

1. 9的平方根是（　　）

A、±3 B、± $\frac{1}{3}$ C、3 D、-3

查看试题解析
2. 下列实数中是无理数的是（）

A、 $\sqrt{9}$ B、 $\frac{22}{7}$ C、π D、( $\sqrt{3}$ )⁰

查看试题解析
3. 下列说法错误的是（）

A、5是25的算术平方根 B、1是1的一个平方根 C、（-4）²的平方根是-4 D、0的平方根与算术平方根都是0

查看试题解析
4. 下列各式中不是二次根式的是（）

A、 $\sqrt{x^{2} + 1}$ B、 $\sqrt{- 4}$ C、 $\sqrt{0}$ D、 $\sqrt{{(a - b)}^{2}}$

查看试题解析
5. 已知实数x，y满足 $\sqrt{x - 2} + {(y + 1)}^{2} = 0$ ，则x﹣y等于（）

A、3 B、﹣3 C、1 D、﹣1

查看试题解析
6. 下列各式化简后，结果为无理数的是（）

A、 $\sqrt{{(- 8)}^{2}}$ B、 $\sqrt[3]{64}$ C、 $\sqrt{9}$ D、 $\sqrt{12}$

查看试题解析
7. 若一个有理数的平方根与立方根是相等的，则这个有理数一定是（　　）

A、0 B、1 C、0或1 D、0和±1

查看试题解析
8. 若m＝ $\sqrt{30}$ －3，则m的范围是（）

A、1＜m＜2 B、2＜m＜3 C、3＜m＜4 D、4＜m＜5

查看试题解析
9. 实数a，b在数轴上的位置如图所示，且|a|＞|b|，则化简 $\sqrt{a^{2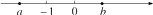}}$ －|a＋b|的结果为（）

A、2a＋b B、－2a＋b C、b D、2a－b

查看试题解析
10. 下列说法正确的个数有（　　）
①2是8的立方根； ②±4是64的立方根； ③无限小数都是无理数； ④带根号的数都是无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 若6－ $\sqrt{13}$ 的整数部分为x，小数部分为y，则(2x＋ $\sqrt{13}$ )y的值是（）

A、5－3 $\sqrt{13}$ B、3 C、3 $\sqrt{13}$ －5 D、－3

查看试题解析

二、填空题

12. 16的平方根是，算术平方根是.

查看试题解析
13. 下列各数： 3 $\sqrt{2}$ ， $- \frac{5}{14}$ ， $\sqrt[3]{- 27}$ ，1.414， $\frac{π}{3}$ ，3.12122， $- \sqrt{9}$ ，3.161661666…（每两个1之间依次多1个6）中，无理数有个，有理数有个，负数有个，整数有个．

查看试题解析
14. 已知x，y都是实数，且y＝ $\sqrt{x - 3}$ ＋ $\sqrt{3 - x}$ ＋4，则y^x＝.

查看试题解析
15. 如果一个正数的平方根是a+3和2a﹣15，则这个数为．

查看试题解析

三、计算题

16. 计算：

(1)、（ $\sqrt{12} + \sqrt{20}$ ）+（ $\sqrt{3} - \sqrt{5}$ ）

(2)、（ $\sqrt{7} - \sqrt{2}$ ）（ $\sqrt{7} + \sqrt{2}$ ）

查看试题解析
17. 求下列各式中x的值：

(1)、(x－2)²＋1＝17；

(2)、(x＋2)³＋27＝0.

查看试题解析
18. 一个数的算术平方根为2M－6，平方根为±(M－2)，求这个数．

查看试题解析
19. 如图，四边形ABCD中，AB＝AD，∠BAD＝90°，若AB＝2 $\sqrt{2}$ ，CD＝4 $\sqrt{3}$ ，BC＝8，求四边形ABCD的面积．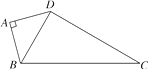

查看试题解析
20. 设 $S_{1} = 1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}$ ， $s_{2} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}$ ， $s_{3} = 1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}$ ，…， $s_{n} = 1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}$ ．若 $s = \sqrt{s_{1}} + \sqrt{s_{2}} + \dots + \sqrt{s_{n}}$ ，求S（用含n的代数式表示，其中n为正整数）．

查看试题解析
21. 用48米长的篱笆在空地上围一个绿化场地，现有两种设计方案：一种是围成正方形场地，另一种是围成圆形场地．选用哪一种方案围成的场地的面积较大？并说明理由．

查看试题解析
22. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋2 $\sqrt{2}$ ＝(1＋ $\sqrt{2}$ )².善于思考的小明进行了以下探索：设a＋b $\sqrt{2}$ ＝(m＋n $\sqrt{2}$ )²(其中a，b，m，n均为整数)，则有a＋b $\sqrt{2}$ ＝m²＋2n²＋2mn $\sqrt{2}$ .∴a＝m²＋2n² ， b＝2mn.这样小明就找到了一种把类似a＋b $\sqrt{2}$ 的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：

(1)、当a，b，m，n均为正整数时，若a＋b $\sqrt{3}$ ＝(m＋n $\sqrt{3}$ )² ，用含m，n的式子分别表示a、b，得a＝， b＝；

(2)、利用所探索的结论，找一组正整数a，b，m，n填空：＋ $\sqrt{3}$ ＝(＋ $\sqrt{3}$ )²；

(3)、若a＋4 $\sqrt{3}$ ＝(m＋n $\sqrt{3}$ )² ，且a，m，n均为正整数，求a的值．

查看试题解析