2018-2019学年数学北师大版九年级上册2.6.1应用一元二次方程 同步训练
试卷更新日期：2018-08-23 类型：同步测试
一、选择题
-
1. 已知△ABC是等腰三角形，BC=8，AB ， AC的长是关于x的一元二次方程x2-10x+k=0的两根，则（ ）
A、k=16 B、k=25 C、k=-16或k=-25 D、k=16或k=252. 现有一块长方形绿地，它的短边长为20 m，若将短边增大到与长边相等(长边不变)，使扩大后的绿地的形状是正方形，则扩大后的绿地面积比原来增加300 m2 ， 设扩大后的正方形绿地边长为xm，下面所列方程正确的是（ ）
A、x(x-20)=300 B、x(x+20)=300 C、60(x+20)=300 D、60(x-20)=3003. 一个等腰三角形的两条边长分别是方程x2-3x+2=0的两根，则该等腰三角形的周长是（ ）A、5或4 B、4 C、5 D、34. 如图，AB⊥BC，AB＝10 cm，BC＝8 cm，一只蝉从C点沿CB方向以每秒1 cm的速度爬行，蝉开始爬行的同时，一只螳螂由A点沿AB方向以每秒2 cm的速度爬行，当螳螂和蝉爬行x秒后，它们分别到达了M，N的位置，此时，△MNB的面积恰好为24 cm2，由题意可列方程（ ）
A、2x·x＝24 B、(10－2x)(8－x)＝24 C、(10－x)(8－2x)＝24 D、(10－2x)(8－x)＝485. 有一块长方形铁皮，长100cm，宽50cm，在它的四周各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为3600cm2 ， 设铁皮各角应切去的正方形边长为xcm，则下面所列方程正确的是（ ）A、4x2=3600 B、100×50﹣4x2=3600 C、（100﹣x）（50﹣x）=3600 D、（100﹣2x）（50﹣2x）=36006. 把一个正方形的一边增加2cm，另一边增加1cm，所得的长方形的面积比正方形面积增加14cm2 ， 那么原来正方形的边长是（ ）
A、3cm B、5cm C、4cm D、6cm7.如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（ ）
A、114 B、124 C、134 D、144二、填空题
-
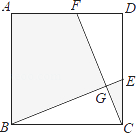
8. 如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为 ．
9. 如图，某小区规划在一个长为16m、宽为9m的矩形场地ABCD上修建三条同样宽的小路，使其中两条与AB平行，另一条与AD平行，其余部分种草．若草坪部分的总面积为112m2 ， 求小路的宽度．若设小路的宽度为xm，则x满足的方程为 ．
10. 如图，在Rt△ABC中，∠B＝90°，AB＝6 cm，BC＝8 cm，点P从A点开始沿AB边向点B以1 cm/s的速度移动，点Q从B点开始沿BC边向点C以2 cm/s的速度移动，则P、Q分别从A、B同时出发，经过秒钟，使△PBQ的面积等于8 cm2.
11. 如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是cm．
12. 如图，将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小正三角形，若 ＝ ， 则正△ABC的边长是 ．
13. 如图，点A的坐标为（﹣4，0），直线y= x+n与坐标轴交于点B、C，连接AC，如果∠ACD=90°，则n的值为 ．
三、解答题
-
14. 如图，某农场有一块长40m， 宽32m的矩形种植地，为方便管理，准备沿平行于两边的方向纵、横各修建一条等宽的小路，要使种植面积为1140m2 ， 求小路的宽
15. 如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．
(1)、当t为何值时，P、Q两点的距离为5 cm？(2)、当t为何值时，△PCQ的面积为15cm2？(3)、请用配方法说明，点P运动多少时间时，四边形BPQA的面积最小？最小面积是多少？16. 如图，等边三角形ABC的边长为6cm，点P自点B出发，以1cm/s的速度向终点C运动；点Q自点C出发，以1cm/s的速度向终点A运动．若P，Q两点分别同时从B，C两点出发，问经过多少时间△PCQ的面积是2 cm2？
17. 在直角墙角AOB（OA⊥OB，且OA、OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m2 ．
(1)、求这地面矩形的长；(2)、有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？18. 如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm．点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，
(1)、如果P、Q同时出发，几秒后，可使△PBQ的面积为8平方厘米？(2)、线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．19. 如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．
(1)、求C点坐标；(2)、求直线MN的解析式；(3)、在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．20. 已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．
(1)、如图①，当∠MAN点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：；(2)、如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；(3)、如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）