人教版初中数学七年级下学期第一次月考试卷

试卷更新日期：2017-02-24 类型：月考试卷

进入出卷网下载

一、单选题

1. (－2)²的算术平方根是（）

A、2 B、±2 C、－2 D、 $\sqrt{2}$

查看试题解析
2. 平面上三条直线两两相交最多能构成对顶角的对数是（）.

A、7 B、6 C、5 D、4

查看试题解析
3. －27的立方根与 $\sqrt{81}$ 的平方根之和是（）

A、0 B、－6 C、0或－6 D、6

查看试题解析
4. 下列语句：①—个数的绝对值—定是正数；② -a—定是—个负数；③绝对值为3的数有两个；④不带根号的数一定是有理数。正确的有 ( )

A、0个 B、1个 C、2个 D、3个

查看试题解析
5.
如图，已知AB∥CD，与∠1是同位角的角是（　　）

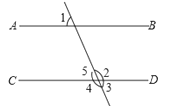A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
6. 若a²=36，b³=8，则a+b的值是（　　）

A、8或﹣4 B、+8或﹣8 C、﹣8或﹣4 D、+4或﹣4

查看试题解析
7. 与无理数 $\sqrt{31}$ 最接近的整数是（　　）

A、4 B、5 C、6 D、7

查看试题解析
8. 在同一平面内，直线a、b相交于O，b∥c，则a与c的位置关系是（　　）

A、平行 B、相交 C、重合 D、平行或重合

查看试题解析
9. 如图，下列说法中错误的是（　　）

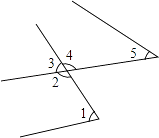A、∠3和∠5是同位角 B、∠4和∠5是同旁内角 C、∠2和∠4是对顶角 D、∠1和∠4是内错角

查看试题解析
10. 过一点画已知直线的平行线，则( )

A、有且只有一条 B、有两条 C、不存在 D、不存在或只有一条

查看试题解析
11. 已知一个表面积为12dm²的正方体，则这个正方体的棱长为（　　）

A、1dm B、 $\sqrt{2}$ dm C、 $\sqrt{6}$ dm D、3dm

查看试题解析
12. 如图，若直线MN与△ABC的边AB、AC分别交于E、F，则图中的内错角有（　　）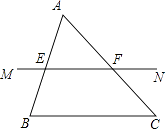

A、2对 B、4对 C、6对 D、8对

查看试题解析

二、填空题

13. 如果一个数的平方根等于这个数的立方根，那么这个数是．

查看试题解析
14. 4的算术平方根是，9的平方根是，﹣27的立方根是．

查看试题解析
15. 如果一个正数的两个平方根是a+6和2a-15，则这个数为 .

查看试题解析
16. 如图所示，与∠C构成同旁内角的有个．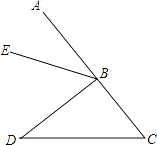

查看试题解析

三、解答题

17. 已知某数的平方根是a+3和2a﹣15，求1﹣7a的立方根．

查看试题解析
18. 如图，BCD是一条直线，∠1=∠B，∠2=∠A，指出∠1的同位角，∠2的内错角，并求出∠A+∠B+∠ACB的度数．

查看试题解析

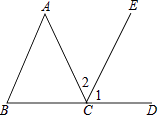
四、综合题

19. 如图，直线AB与CD相交于点O，OP是∠BOC的平分线，OE⊥AB，OF⊥CD，

(1)、图中除直角外，还有相等的角吗？请写出两对：①；② ．

(2)、如果∠AOD＝40°，则①∠BOC＝；②OP是∠BOC的平分线，所以∠COP＝度；③求∠BOF的度数．

查看试题解析
20. 阅读以下两小题后作出相应的解答：

(1)、“同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等“的逆命题，并指出逆命题的题设和结论；

(2)、根据以下语句作出图形，并写出该命题的文字叙述.
已知：过直线AB上一点O任作射线OC ， OM、ON分别平分∠AOC、∠BOC ，则OM⊥ON ．

查看试题解析
21. 直线AB、CD相交于点O.OE、OF分别是∠AOC、∠BOD的平分线.

(1)、画出这个图形.

(2)、射线OE、OF在同一条直线上吗?

(3)、画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.

查看试题解析
22. 数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人十分惊奇，忙问计算的奥妙．你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：

(1)、10³=1000，100³=1000000，你能确定59319的立方根是几位数吗？答：位数．

(2)、由59319的个位数是9，你能确定59319的立方根的个位数是几吗？答：

(3)、如果划去59319后面的三位319得到数59，而3³=27，4³=64，由此你能确定59319的立方根的十位数是几吗？答：．因此59319的立方根是．

(4)、现在换一个数185193，你能按这种方法说出它的立方根吗？
答：①它的立方根是位数，②它的立方根的个位数是， ③它的立方根的十位数是， ④185193的立方根是．

查看试题解析
23.
如图(2)

(1)、如果∠1=∠D，那么∥；

(2)、如果∠1=∠B，那么∥；

(3)、如果∠A+∠B=18 0º，那么∥；

(4)、如果∠A+∠D=180º，那么∥；

查看试题解析
24. 如图（1），AB∥CD，猜想∠BPD与∠B，∠D的关系，说出理由．
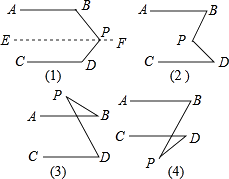
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°（两直线平行，同旁内角互补）
∵AB∥CD，EF∥AB，
∴EF∥CD，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行．）
∴∠EPD+∠D=180°（两直线平行，同旁内角互补）
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°

(1)、依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，并说明理由．

(2)、观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B，∠D的关系，不需要说明理由．

查看试题解析