2016-2017学年浙江省嘉兴市桐乡市现代片四校九年级上学期期中数学试卷

试卷更新日期：2017-02-23 类型：期中考试

进入出卷网下载

一、选择题

1. 抛物线y=﹣（x+2）²﹣3的顶点坐标是（）

A、（2，﹣3） B、（﹣2，3） C、（2，3） D、（﹣2，﹣3）

查看试题解析
2. 如图，点A，B，C是⊙O上三点，∠AOC=130°，则∠ABC等于（）

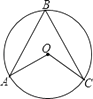A、50° B、60° C、65° D、70°

查看试题解析
3. “a是实数，|a|≥0”这一事件是（）

A、必然事件 B、不确定事件 C、不可能事件 D、随机事件

查看试题解析
4. 小强、小亮、小文三位同学玩投硬币游戏．三人同时各投出一枚均匀硬币，若出现三个正面向上或三个反面向上，则小强赢；若出现2个正面向上一个反面向上，则小亮赢；若出现一个正面向上2个反面向上，则小文赢．下面说法正确的是（）

A、三人赢的概率都相等 B、小文赢的概率最小 C、小亮赢的概率最小 D、小强赢的概率最小

查看试题解析
5. 有下列四个命题，其中正确的有（　　）
①圆的对称轴是直径； ②经过三个点一定可以作圆；
③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．

A、4个 B、3个 C、2个 D、1个

查看试题解析
6.
二次函数y=ax²+bx+c的图像如图所示，则反比例函数 $y = \frac{a}{x}$ 与一次函数y=bx+c在同一坐标系中的大致图像是（）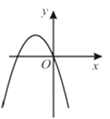

A、 B、 C、 D、

查看试题解析
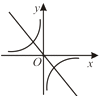7. 在平面直角坐标系中，将抛物线y=x²+2x+3绕着原点旋转180°，所得抛物线的解析式是（）

A、y=﹣（x﹣1）²﹣2 B、y=﹣（x+1）²﹣2 C、y=﹣（x﹣1）²+2 D、y=﹣（x+1）²+2

查看试题解析
8. 已知函数y=3x²﹣6x+k（k为常数）的图像经过点A（0.8，y₁），B（1.1，y₂），C（ $\sqrt{2}$ ，y₃），则有（）

A、y₁＜y₂＜y₃ B、y₁＞y₂＞y₃ C、y₃＞y₁＞y₂ D、y₁＞y₃＞y₂

查看试题解析
9. 已知⊙O的半径为5，点O到弦AB的距离为3，则⊙O上到弦AB所在直线的距离为2的点有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 当﹣2≤x≤1时，二次函数y=﹣（x﹣m）²+m²+1有最大值4，则实数m的值为（）

A、﹣ $\frac{7}{4}$ B、 $\sqrt{3}$ 或﹣ $\sqrt{3}$ C、2或﹣ $\sqrt{3}$ D、2或﹣ $\sqrt{3}$ 或﹣ $\frac{7}{4}$

查看试题解析

二、填空题

11. 一个黑袋中装有3个红球和5个白球，它们除颜色外其余都相同．从中任意摸出一个球，是红球的概率

查看试题解析
12. 抛物线y= $\frac{1}{2}$ x²的开口方向，顶点坐标是．

查看试题解析
13. 从标有1，2，3，4的四张卡片中任取两张，卡片上的数字之和为奇数的概率是．

查看试题解析
14. 将抛物线y=﹣x²先向右平移1个单位，再向上平移5个单位，得到的抛物线的解析式是

查看试题解析
15. 把二次函数y=﹣2x²+4x+3化成y=a（x﹣m）²+k的形式是．

查看试题解析
16. 如图，AB是⊙O的弦，OC⊥AB于C．若AB=2 $\sqrt{3}$ ，OC=1，则半径OB的长为

查看试题解析
17. 如图，点A，B，C，D在⊙O上，点O在∠D的内部，四边形OABC为平行四边形，则∠OAD+∠OCD=°．

查看试题解析
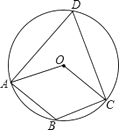18. 如图，AB是⊙O的直径，点C，D是圆上两点，∠AOC=100°，则∠D=度．

查看试题解析
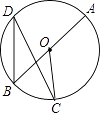19. 如图，一名男生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y=﹣ $\frac{1}{12}$ x²+ $\frac{2}{3}$ x+ $\frac{5}{3}$ ．则他将铅球推出的距离是 m．

查看试题解析
20.
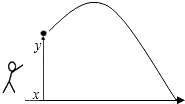二次函数 $y = \frac{2}{3} x^{2}$ 的图像如图所示，点A₀位于坐标原点，点A₁ ， A₂ ， A₃ ， …，A₂₀₀₈在y轴的正半轴上，点B₁ ， B₂ ， B₃ ， …，B₂₀₀₈在二次函数 $y = \frac{2}{3} x^{2}$ 位于第一象限的图像上，若△A₀B₁A₁ ， △A₁B₂A₂ ， △A₂B₃A₃ ， …，△A₂₀₀₇B₂₀₀₈A₂₀₀₈都为等边三角形，则△A₂₀₀₇B₂₀₀₈A₂₀₀₈的边长=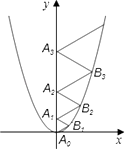

查看试题解析

三、解答题

21. 已知抛物线y=x²﹣4x+c，经过点（0，9）．

(1)、求c的值；

(2)、若点A（3，y₁）、B（4，y₂）在该抛物线上，试比较y₁、y₂的大小．

查看试题解析
22. 某篮球运动员带了2件上衣和3条短裤（上衣和短裤分别装在两个包里），上衣的颜色是红色和白色，短裤的颜色是红色、白色、黄色．

(1)、他随意拿出一件上衣和一条短裤配成一套，用画树状图或列表的方法列出所有可能出现的结果．

(2)、他随意拿出一件上衣和一条短裤，颜色正好相同的概率是多少？

查看试题解析
23. 如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC交⊙O于点F．

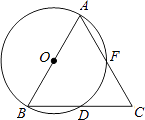(1)、AB与AC的大小有什么关系？为什么？

(2)、若∠BAC=70°，求弧BD、弧DF和弧AF的度数．

查看试题解析
24. 一跨河桥，桥拱是圆弧形，跨度（AB）为16米，拱高（CD）为4米，求：

(1)、桥拱半径

(2)、若大雨过后，桥下河面宽度（EF）为12米，求水面涨高了多少？

查看试题解析
25. 某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．

(1)、写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；

(2)、求销售单价为多少元时，该文具每天的销售利润最大；

(3)、商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元
请比较哪种方案的最大利润更高，并说明理由．

查看试题解析
26.
如图，抛物线y=﹣ $\frac{1}{2}$ x²+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．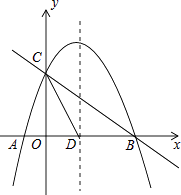

(1)、求抛物线的表达式；

(2)、在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；

(3)、点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

查看试题解析