2016-2017学年浙江省杭州市余杭区九年级上学期期中数学试卷
试卷更新日期：2017-02-23 类型：期中考试
一、选择题
-
1. 下列函数解析式中，一定为二次函数的是（ ）
A、y=3x﹣1 B、y=ax2+bx+c C、s=2t2﹣2t+1 D、y=x2+2. 下列事件是必然事件的是（ ）A、若a是实数，则|a|≥0 B、抛一枚硬币，正面朝上 C、明天会下雨 D、打开电视，正在播放新闻3. 已知一个二次函数y=ax2（a≠0）的图像经过（﹣2，6），则下列点中不在该函数的图象上的是（ ）A、（2，6） B、（1，1.5） C、（﹣1，1.5） D、（2，8）4. 下列说法正确的是（ ）A、半圆是弧，弧也是半圆 B、三点确定一个圆 C、平分弦的直径垂直于弦 D、直径是同一圆中最长的弦5. 设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+3上的三点，则y1 ， y2 ， y3的大小关系为（ ）A、y1＞y2＞y3 B、y1＞y3＞y2 C、y3＞y2＞y1 D、y3＞y1＞y26. 如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8，CD=3，则⊙O的半径为（ ）
A、4 B、5 C、 D、7. 在一个不透明的盒子中装有n个小球，它们除了颜色不同外，其余都相同，其中有4个白球，每次试验前，将盒子中的小球摇匀，随机摸出一个球记下颜色后再放回盒中．大量重复上述试验后发现，摸到白球的频率稳定在0.4，那么可以推算出n大约是（ ）A、10 B、14 C、16 D、408. 如图所示的暗礁区，两灯塔A，B之间的距离恰好等于圆的半径，为了使航船（S）不进入暗礁区，那么S对两灯塔A，B的视角∠ASB必须（ ）
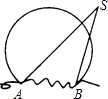A、大于60° B、小于60° C、大于30° D、小于30°9. 如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）
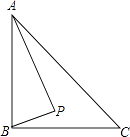A、 B、2 C、 D、10. 如图，直线y=kx+c与抛物线y=ax2+bx+c的图像都经过y轴上的D点，抛物线与x轴交于A、B两点，其对称轴为直线x=1，且OA=OD．直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确命题的是（ ）①abc＞0； ②3a+b＞0； ③﹣1＜k＜0； ④4a+2b+c＜0； ⑤a+b＜k．
A、①②③ B、②③⑤ C、②④⑤ D、②③④⑤二、填空题
-
11. 从长度为2，3，5，7的四条线段中任意选取三条，这三条线段能构成三角形的概率等于 ．12. 抛物线y=﹣（x﹣2）2+1的顶点坐标是13. 已知△ABC的边BC=2 cm，且△ABC内接于半径为2cm的⊙O，则∠A=度．14. 如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数为90°，则∠B的度数是 ．
15. 已知AB是⊙O的直径，弦CD⊥AB于点E，弦PQ∥AB交弦CD于点M，BE=18，CD=PQ=24，则OM的长为 ．
16.在第一象限内作射线OC，与x轴的夹角为60°，在射线OC上取一点A，过点A作AH⊥x轴于点H，在抛物线y=x2（x＞0）上取一点P，在y轴上取一点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是
三、解答题
-
17. 如图，
(1)、作△ABC的外接⊙O（用尺规作图，保留作图痕迹，不写作法）；(2)、若AB=6cm，AC=BC=5cm，求⊙O的半径．18. 甲、乙两人同在如图所示的地下车库等电梯，两人到1至4层的任意一层出电梯，
(1)、请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率；(2)、小亮和小芳打赌说：“若甲、乙在同一层或相邻楼层出电梯，则小亮胜，否则小芳胜”．该游戏是否公平？说明理由．19. 如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：AD=CE．
20. 如图，在平面直角坐标系内，已知点A（2，2），B（﹣6，﹣4），C（2，﹣4）．
(1)、求△ABC的外接圆的圆心点M的坐标；(2)、求△ABC的外接圆在x轴上所截弦DE的长．21. 一座桥如图，桥下水面宽度AB是20米，高CD是4米．要使高为3米的船通过，则其宽度须不超过多少米．
(1)、如图1，若把桥看做是抛物线的一部分，建立如图坐标系．①求抛物线的解析式； ②要使高为3米的船通过，则其宽度须不超过多少米？
(2)、如图2，若把桥看做是圆的一部分．①求圆的半径；②要使高为3米的船通过，则其宽度须不超过多少米？
22.如图，在平面直角坐标系中，将一块腰长为 的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（﹣1，0），点B在抛物线y=ax2+ax﹣2上．
(1)、点A的坐标为 ， 点B的坐标为；(2)、抛物线的解析式为；(3)、设（2）中抛物线的顶点为D，求△DBC的面积；(4)、在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．