2016-2017学年浙江省杭州市萧山区城北片九年级上学期期中数学试卷

试卷更新日期：2017-02-23 类型：期中考试

进入出卷网下载

一、仔细选一选

1. 从1～9这九个自然数中任取一个，是2的倍数的概率是（）

A、 $\frac{2}{9}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{2}{3}$

查看试题解析
2. 如图，⊙O的半径为5，AB为弦，半径OC⊥AB，垂足为点E，若OE=3，则AB的长是（）

A、4 B、6 C、8 D、10

查看试题解析
3. 由二次函数y=2（x﹣3）²+1，可知（）

A、其图像的开口向下 B、其图像的对称轴为直线x=﹣3 C、其最小值为1 D、当x＜3时，y随x的增大而增大

查看试题解析
4. 与y=2（x﹣1）²+3形状相同的抛物线解析式为（　　）

A、y=1+ $\frac{1}{2}$ x² B、y=（2x+1）² C、y=（x﹣1）² D、y=2x²

查看试题解析
5. 下列命题正确的是（）

A、相等的圆周角对的弧相等 B、等弧所对的弦相等 C、三点确定一个圆 D、平分弦的直径垂直于弦

查看试题解析
6. 在同一直角坐标系中，函数y=mx+m和y=﹣mx²+2x+2（m是常数，且m≠0）的图像可能是（）

A、 B、 C、 D、

查看试题解析
7. 已知二次函数y=﹣ $\frac{1}{2}$ x²﹣3x﹣ $\frac{5}{2}$ ，设自变量的值分别为x₁ ， x₂ ， x₃ ，且﹣3＜x₁＜x₂＜x₃ ，则对应的函数值y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＞y₂＞y₃ B、y₁＜y₂＜y₃ C、y₂＞y₃＞y₁ D、y₂＜y₃＜y₁

查看试题解析
8. 若二次函数y=ax²﹣2ax+c的图像经过点（﹣1，0），则方程ax²﹣2ax+c=0的解为（）

A、x₁=﹣3，x₂=﹣1 B、x₁=1，x₂=3 C、x₁=﹣1，x₂=3 D、x₁=﹣3，x₂=1

查看试题解析
9. 已知⊙O的半径为3，△ABC内接于⊙O，AB=3 $\sqrt{2}$ ，AC=3 $\sqrt{3}$ ，D是⊙O上一点，且AD=3，则CD的长应是（）

A、3 B、6 C、 $\sqrt{3}$ D、3或6

查看试题解析
10. 二次函数y=ax²+bx+c（a＞0）的顶点为P，其图像与x轴有两个交点A（﹣m，0），B（1，0），交y轴于点C（0，﹣3am+6a），以下说法：
①m=3；
②当∠APB=120°时，a= $\frac{\sqrt{3}}{6}$ ；
③当∠APB=120°时，抛物线上存在点M（M与P不重合），使得△ABM是顶角为120°的等腰三角形；
④抛物线上存在点N，当△ABN为直角三角形时，有a≥ $\frac{1}{2}$
正确的是（）

A、①② B、③④ C、①②③ D、①②③④

查看试题解析

二、认真填一填

11. 若函数y=（m﹣1）x^|^m^|+¹是二次函数，则m的值为．

查看试题解析
12. 如图，AB是半圆的直径，∠BAC=20°，D是 $\hat{A C}$ 的中点，则∠DAC的度数是．

查看试题解析
13. 把一个体积是64立方厘米的立方体木块的表面涂上红漆，然后锯成体积为1立方厘米的小立方体，从中任取一块，则取出的这一块至少有一面涂红漆的概率是．

查看试题解析
14. 如图，抛物线y=ax²+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a﹣2b+c的值为

查看试题解析
15. △ABC的一边长为5，另两边长分别是二次函数y=x²﹣6x+m与x轴的交点坐标的横坐标的值，则m的取值范围为

查看试题解析
16. 如图，在平面直角坐标系中，点A的坐标是（4，3），动圆D经过A，O，分别与两坐标轴的正半轴交于点E，F．当EF⊥OA时，此时EF= ．

查看试题解析

三、全面答一答

17.
小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上．

(1)、请你帮小明把花坛的位置画出来（尺规作图，不写作法，保留作图痕迹）．

(2)、在△ABC中，AC=4米，∠ABC=45°，试求小明家圆形花坛的半径长．

查看试题解析
18. 在1个不透明的口袋里，装有红、白、黄三种颜色的乒乓球（除颜色外，其余都相同），其中有白球2个，黄球1个，若从中任意摸出一个球，这个球是白色的概率为0.5．

(1)、求口袋中红球的个数；

(2)、若摸到红球记0分，摸到白球记1分，摸到黄球记2分，甲从口袋中摸出一个球，不放回，再找出一个画树状图的方法求甲摸的两个球且得2分的概率．

查看试题解析
19. 如图，AB是⊙O的直径，C、D两点在⊙O上，若∠C=45°，

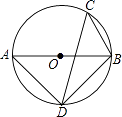(1)、求∠ABD的度数．

(2)、若∠CDB=30°，BC=3，求⊙O的半径．

查看试题解析
20. 如图，已知抛物线y=﹣x²+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0）

(1)、求m的值及抛物线的顶点坐标．

(2)、点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．

查看试题解析
21. 已知：如图，在半径为2的半圆O中，半径OA垂直于直径BC，点E与点F分别在弦AB、AC上滑动并保持AE=CF，但点F不与A、C重合，点E不与A、B重合．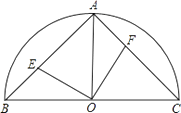

(1)、求四边形AEOF的面积．

(2)、设AE=x，S_△_OEF=y，写出y与x之间的函数关系式，求x取值范围．

查看试题解析
22. 某景点试开放期间，团队收费方案如下：不超过30人时，人均收费120元；超过30人且不超过m（30＜m≤100）人时，每增加1人，人均收费降低1元；超过m人时，人均收费都按照m人时的标准．设景点接待有x名游客的某团队，收取总费用为y元．

(1)、求y关于x的函数表达式；

(2)、景点工作人员发现：当接待某团队人数超过一定数量时，会出现随着人数的增加收取的总费用反而减少这一现象．为了让收取的总费用随着团队中人数的增加而增加，求m的取值范围．

查看试题解析
23.
如图，直线l：y=﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y=ax²﹣2ax+a+4（a＜0）经过点B．

(1)、求该抛物线的函数表达式；

(2)、已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值；

(3)、在（2）的条件下，当S取得最大值时，动点M相应的位置记为点M′．
①写出点M′的坐标；
②将直线l绕点A按顺时针方向旋转得到直线l′，当直线l′与直线AM′重合时停止旋转，在旋转过程中，直线l′与线段BM′交于点C，设点B、M′到直线l′的距离分别为d₁、d₂ ，当d₁+d₂最大时，求直线l′旋转的角度（即∠BAC的度数）．

查看试题解析