2016-2017学年浙江省杭州市上城区九年级上学期期中数学试卷
试卷更新日期:2017-02-23 类型:期中考试
一、选择题
-
1. 把抛物线y=3x2向上平移一个单位,则所得抛物线的解析式为( )A、y=3(x+1)2 B、y=3x2+1 C、y=3(x﹣1)2 D、y=3x2﹣12. 一个不透明的袋子中装有5个黑球和3个白球,这些球的大小、质地完全相同,随机从袋子中摸出4个球,则下列事件是必然事件的是( )A、摸出的四个球中至少有一个球是白球 B、摸出的四个球中至少有一个球是黑球 C、摸出的四个球中至少有两个球是黑球 D、摸出的四个球中至少有两个球是白球3. 若⊙P的半径为13,圆心P的坐标为(5,12),则平面直角坐标系的原点O与⊙P的位置关系是( )A、在⊙P内 B、在⊙P上 C、在⊙P外 D、无法确定4. 有长度分别为2cm,3cm,4cm,7cm的四条线段,任取其中三条能组成三角形的概率是( )A、 B、 C、 D、5. 如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( )
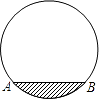 A、2m B、2.5m C、4m D、5m6. 下列说法不正确的是( )A、圆是轴对称图形,它有无数条对称轴 B、圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边 C、弦长相等,则弦所对的弦心距也相等 D、垂直于弦的直径平分这条弦,并且平分弦所对的弧7. 连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )A、
A、2m B、2.5m C、4m D、5m6. 下列说法不正确的是( )A、圆是轴对称图形,它有无数条对称轴 B、圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边 C、弦长相等,则弦所对的弦心距也相等 D、垂直于弦的直径平分这条弦,并且平分弦所对的弧7. 连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图(扇形、菱形、直角梯形、红十字图标)中“直径”最小的是( )A、 B、
B、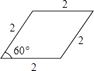 C、
C、 D、
D、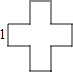 8. 已知二次函数y=﹣ x2﹣3x﹣ ,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1<y2<y3 C、y2>y3>y1 D、y2<y3<y19. 已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值y<0,那么下列结论中正确的是( )A、m﹣1的函数值小于0 B、m﹣1的函数值大于0 C、m﹣1的函数值等于0 D、m﹣1的函数值与0的大小关系不确定10. 二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
8. 已知二次函数y=﹣ x2﹣3x﹣ ,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1<y2<y3 C、y2>y3>y1 D、y2<y3<y19. 已知二次函数y=x2﹣x+a(a>0),当自变量x取m时,其相应的函数值y<0,那么下列结论中正确的是( )A、m﹣1的函数值小于0 B、m﹣1的函数值大于0 C、m﹣1的函数值等于0 D、m﹣1的函数值与0的大小关系不确定10. 二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:①m=3;
②当∠APB=120°时,a= ;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥
正确的是( )
A、①② B、③④ C、①②③ D、①②③④二、填空题
-
11. 将y=2x2﹣12x﹣12变为y=a(x﹣m)2+n的形式,则m•n= .12. ⊙O的直径为10,弦AB=6,P是弦AB上一动点,则OP的取值范围是13. 甲、乙玩猜数字游戏,游戏规则如下:有四个数字0、1、2、3,先由甲心中任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为n.若m、n满足|m﹣n|≤1,则称甲、乙两人“心有灵犀”,则甲、乙两人“心有灵犀”的概率是 .14. 函数y=x2+bx+c与y=x的图像如图所示,有以下结论:
①b2﹣4c>0;②3b+c+6=0;③当1<x<3时,x2+(b﹣1)x+c<0;
④ ,其中正确的有
 15. 已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为16. 如图,在等腰Rt△ABC中,AC=BC=2 ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是
15. 已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为16. 如图,在等腰Rt△ABC中,AC=BC=2 ,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是
三、解答题
-
17. 如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
 (1)、任意闭合其中一个开关,则小灯泡发光的概率等于;(2)、任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.18. 已知二次函数的顶点坐标为(2,﹣2),且其图像经过点(3,1),求此二次函数的解析式,并求出该函数图象与y轴的交点坐标.19. 如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.
(1)、任意闭合其中一个开关,则小灯泡发光的概率等于;(2)、任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.18. 已知二次函数的顶点坐标为(2,﹣2),且其图像经过点(3,1),求此二次函数的解析式,并求出该函数图象与y轴的交点坐标.19. 如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.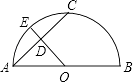 20. 已知函数y=mx2﹣6x+1(m是常数).(1)、求证:不论m为何值,该函数的图象都经过y轴上的一个定点;(2)、若该函数的图象与x轴只有一个交点,求m的值.21. 高致病性禽流感是比SARS传染速度更快的传染病.为防止禽流感蔓延,政府规定:离疫点3km范围内为扑杀区;离疫点3km~5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
20. 已知函数y=mx2﹣6x+1(m是常数).(1)、求证:不论m为何值,该函数的图象都经过y轴上的一个定点;(2)、若该函数的图象与x轴只有一个交点,求m的值.21. 高致病性禽流感是比SARS传染速度更快的传染病.为防止禽流感蔓延,政府规定:离疫点3km范围内为扑杀区;离疫点3km~5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km. (1)、请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);(2)、求这条公路在免疫区内有多少千米?22. 如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系
(1)、请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);(2)、求这条公路在免疫区内有多少千米?22. 如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系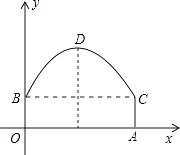 (1)、求该抛物线的解析式.(2)、一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?(3)、在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米?23. 如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,
(1)、求该抛物线的解析式.(2)、一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?(3)、在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米?23. 如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,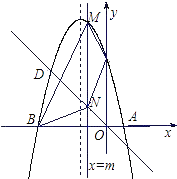 (1)、求该抛物线的解析式;(2)、设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)、设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线 与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)、设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线 与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.