2018-2019学年数学浙教版九年级上册1.4 二次函数的应用（3）同步练习

试卷更新日期：2018-08-21 类型：同步测试

进入出卷网下载

一、选择题

1. 如果将抛物线y=x²+2向下平移1个单位，那么所得新抛物线的表达式是（）

A、y=（x-1）²+2 B、y=（x+1）²+2 C、y=x²+1 D、y=x²+3

查看试题解析
2. 如图，从地面竖直向上抛出一个小球，小球的高度 $h ($ 单位：m $)$ 与小球运动时间 $t ($ 单位： $s)$ 之间的函数关系式为 $h = 30 t - 5 t^{2}$ ，那么小球从抛出至回落到地面所需的时间是（）

A、6s B、4s C、3s D、2s

查看试题解析
3. 二次函数 $y = x^{2} - 2 x - 3$ 的图象如图所示．当y＜0时，自变量x的取值范围是（）．

A、－1＜x＜3 B、x＜－1 C、x＞3 D、x＜－1或x＞3

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴是直线x=﹣1及部分图像（如图所示），由图像可知关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两个根分别是 $x_{1} = 1.3$ 和 $x_{2} =$ （）

A、﹣1.3 B、﹣2.3 C、﹣3.3 D、﹣4.3

查看试题解析
5. 已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数y=﹣ $\frac{1}{3}$ x²+2x+5 图象的一部分，其中x为爆炸后经过的时间（秒），y为残片离地面的高度（米），请问在爆炸后1秒到6秒之间，残片距离地面的高度范围为（）

A、0米到8米 B、5米到8米 C、 $\frac{20}{3}$ 到8米 D、5米到 $\frac{20}{3}$ 米

查看试题解析
6. 小明利用二次函数的图象估计方程x²－2x－2＝0的近似解，如表是小明探究过程中的一些计算数据．根据表中数据可知，方程x²－2x－2＝0必有一个实数根在（）
x
1.5
2
2.5
3
3.5
x²－2x－2
－2.75
－2
－0.75
1
3.25

A、1.5和2之间 B、2和2.5之间 C、2.5和3之间 D、3和3.5之间

查看试题解析
7. 根据抛物线y＝x²＋3x－1与x轴的交点的坐标，可以求出下列方程中哪个方程的近似解（）

A、x²＋3x－1＝0 B、x²＋3x＋1＝0 C、3x²＋x－1＝0 D、x²－3x＋1＝0

查看试题解析
8. 某工厂2015年产品的产量为100吨，该产品产量的年平均增长率为x(x＞0)，设2017年该产品的产量为y吨，则y关于x的函数关系式为（）

A、y＝100(1－x)² B、y＝100(1＋x)² C、y＝ $\frac{100}{{(1 + x)}^{2}}$ D、y＝100＋100(1＋x)＋100(1＋x)²

查看试题解析
9. 在羽毛球比赛中，某次羽毛球的运动路线可以看做是抛物线y＝－ $\frac{1}{4}$ x²＋bx＋c的一部分(如图)，其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，那么这条抛物线的表达式是（）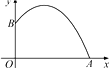

A、y＝－ $\frac{1}{4}$ x²＋ $\frac{3}{4}$ x＋1 B、y＝－ $\frac{1}{4}$ x²＋ $\frac{3}{4}$ x－1 C、y＝－ $\frac{1}{4}$ x²－ $\frac{3}{4}$ x＋1 D、y＝－ $\frac{1}{4}$ x²－ $\frac{3}{4}$ x－1

查看试题解析
10. 某地要建造一个圆形喷水池，在水池中央垂直于地面安装一个柱子OA，O恰为水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上，建立平面直角坐标系（如图），水流喷出的高度y（m）与水平距离x（m）之间的关系式是 $y = - x^{2} + 2 x + 3$ ，则下列结论：（1）柱子OA的高度为3m；（2）喷出的水流距柱子1m处达到最大高度；（3）喷出的水流距水平面的最大高度是4m；（4）水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有（）

A、1个 B、2个 C、3个 D、4

查看试题解析

二、填空题

11. 已知二次函数y=ax²+bx+c（a≠0）中，函数值y与自变量x的部分对应值如下表：
则关于x的一元二次方程ax²+bx+c=﹣2的根是．
x
…
-5
-4
-3
-2
-1
…
y
…
3
-2
-5
-6
-5
…

查看试题解析
12. 农机厂第一个月水泵的产量为50（台），第三个月的产量y（台）与月平均增长率x之间的关系表示为．

查看试题解析
13. 某圆形喷水池的水柱如图①所示，如果曲线APB表示落点B离点O最远的一条水流，如图②所示，其上的水珠的高度y(米)关于水平距离x(米)的函数解析式为y=－x²＋4x＋ $\frac{9}{4}$ ，那么圆形水池的半径至少为米时，才能使喷出的水流不落在水池外．

查看试题解析
14. 2013年5月26日，中国羽毛球队蝉联苏迪曼杯团体赛冠军，成就了首个五连冠霸业．比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图)，若不考虑外力因素，羽毛球行进高度y(米)与水平距离x(米)之间满足关系y＝－ $\frac{2}{9}$ x²＋ $\frac{8}{9}$ x＋ $\frac{10}{9}$ ，则羽毛球飞出的水平距离为米．

查看试题解析
15. 二次函数y=ax²+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论：
①ac＜0；②当x＞1时，y的值随x值的增大而减小；
③当 $x = 2$ 时， $y = 5$ ；④3是方程ax²+（b﹣1）x+c=0的一个根.
其中正确的结论是（填正确结论的序号）.

查看试题解析
16. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，若方程 $a x^{2} + b x + c = k$ 有两个不相等的实数根，则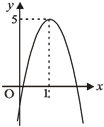 $k$ 的取值范围是。

查看试题解析

三、解答题

17. 如图，二次函数y=(x-2)²+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点，已知一次函数y=kx+b的图象上的点A（1，0）及B.

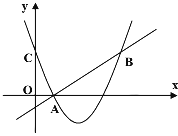(1)、求二次函数与一次函数的解析式；

(2)、根据图象，写出满足kx+b≤（x-2）²+m的x的取值范围.

查看试题解析
18. 小明在一次打篮球时，篮球传出后的运动路线为如图所示的抛物线，以小明所站立的位置为原点O建立平面直角坐标系，篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=- $\frac{1}{8}$ x²+x+c.

(1)、求y与x之间的函数表达式；

(2)、球在运动的过程中离地面的最大高度；

(3)、小亮手举过头顶，跳起后的最大高度为BC=2.5m，若小亮要在篮球下落过程中接到球，求小亮离小明的最短距离OB.

查看试题解析
19. 足球比赛中，某运动员将在地面上的足球对着球门踢出，图中的抛物线是足球的飞行高度y（m）关于飞行时间x（s）的函数图象（不考虑其它因素），已知足球飞出1s时，足球的飞行高度是2.44m，足球从飞出到落地共用3s．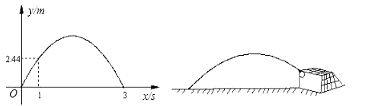

(1)、求y关于x的函数解析式；

(2)、足球的飞行高度能否达到4.88 m？请说明理由；

(3)、假设没有拦挡，足球将擦着球门左上角射入球门，球门的高为2.44 m（如图所示，足球的大小忽略不计）．如果为了能及时将足球扑出，那么足球被踢出时，离球门左边框12m处的守门员至少要在几s内到球门的左边框？

查看试题解析
20. 某广场喷泉的喷嘴安装在平地上．有一喷嘴喷出的水流呈抛物线状，喷出的水流高度y（m）与喷出水流喷嘴的水平距离x（m）之间满足 $y = - \frac{1}{2} x^{2} + 2 x$

(1)、喷嘴能喷出水流的最大高度是多少？

(2)、喷嘴喷出水流的最远距离为多少？

查看试题解析
21. 已知抛物线 $y = a x^{2} + b x + c$ (a、b、c是常数， $a \neq 0$ )的对称轴为直线 $x = - 2$ ．

(1)、b=；(用含a的代数式表示)

(2)、当 $a = - 1$ 时，若关于x的方程 $a x^{2} + b x + c = 0$ 在 $- 3 < x < 1$ 的范围内有解，求c的取值范围；

(3)、若抛物线过点( $- 2$ ， $- 2$ )，当 $- 1 \leq x \leq 0$ 时，抛物线上的点到x轴距离的最大值为4，求a的值．

查看试题解析
22. 根据下列要求，解答相关问题．

(1)、请补全以下求不等式 $x^{2} - 2 x < 0$ 的解集的过程：
① 构造函数，画出图象：根据不等式特征构造二次函数y= $x^{2} - 2 x$ ；并在下面的坐标系中（图1）画出二次函数y= $x^{2} - 2 x$ 的图象（只画出大致图象即可）；
② 求得界点，标示所需：当 $y = 0$ 时，求得方程 $x^{2} - 2 x = 0$ 的解为；并用虚线标示出函数y= $x^{2} - 2 x$ 图象中 $y$ ＜0的部分；
③借助图象，写出解集：由所标示图象，可得不等式 $x^{2} - 2 x$ ＜0的解集为．

(2)、请你利用上面求不等式解集的过程，求不等式 $x^{2} - 2 x$ -3≥0的解集．

查看试题解析

x	1.5	2	2.5	3	3.5
x²－2x－2	－2.75	－2	－0.75	1	3.25

x	…	-5	-4	-3	-2	-1	…
y	…	3	-2	-5	-6	-5	…

x	﹣1	0	1	3
y	﹣1	3	5	3

2018-2019学年数学浙教版九年级上册1.4 二次函数的应用（3） 同步练习

一、选择题

二、填空题

三、解答题

2018-2019学年数学浙教版九年级上册1.4 二次函数的应用（3）同步练习