2018-2019学年数学人教版九年级上册22.3 实际问题与二次函数（1） 同步训练
试卷更新日期：2018-08-21 类型：同步测试
一、选择题
-
1. 如图，从地面竖直向上抛出一个小球，小球的高度 单位：m 与小球运动时间 单位： 之间的函数关系式为 ，那么小球从抛出至回落到地面所需的时间是（ ）
A、6s B、4s C、3s D、2s2. 某海滨浴场有100个遮阳伞，每个每天收费10元时，可全部租出；若每个每天提高2元，则减少10个伞租出，若每个每天收费再提高2元，则再减少10个伞租出……为了投资少而获利大，每个每天应提高（ ）
A、4元或6元 B、4元 C、6元 D、8元3. 已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数y=﹣ x2+2x+5 图象的一部分，其中x为爆炸后经过的时间（秒），y为残片离地面的高度（米），请问在爆炸后1秒到6秒之间，残片距离地面的高度范围为（ ）
A、0米到8米 B、5米到8米 C、 到8米 D、5米到 米4. 某工厂2015年产品的产量为100吨，该产品产量的年平均增长率为x(x＞0)，设2017年该产品的产量为y吨，则y关于x的函数关系式为（ ）
A、y＝100(1－x)2 B、y＝100(1＋x)2 C、y＝ D、y＝100＋100(1＋x)＋100(1＋x)25. 某农产品市场经销一种销售成本为40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨一元，月销售量就减少10千克．设销售单价为每千克x元，月销售利润为y元，则y与x的函数关系式为（ ）
A、 B、 C、 D、6. 某品牌钢笔进价8元，按10元1支出售时每天能卖出20支，市场调查发现如果每支每涨价1元，每天就少卖出2支，为了每天获得最大利润，其售价应定为（ ）
A、11元 B、12元 C、13元 D、14元7. 某地要建造一个圆形喷水池，在水池中央垂直于地面安装一个柱子OA，O恰为水面中心，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上，建立平面直角坐标系（如图），水流喷出的高度y（m）与水平距离x（m）之间的关系式是 ，则下列结论：（1）柱子OA的高度为3m；（2）喷出的水流距柱子1m处达到最大高度；（3）喷出的水流距水平面的最大高度是4m；（4）水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个8. 某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y（件）与销售单价x（元/件）之间的函数关系式为y=–4x+440，要获得最大利润，该商品的售价应定为（ ）
A、60元 B、70元 C、80元 D、90元二、填空题
-
9. 某纸箱厂第1年的利润为50万元，如果每一年比上一年的利润增长率相同，都是x，则第3年的利润为万元。
10. 红光旅行社有100张床位，每床每日收费10元，客床可全部租出，若每床每日收费提高2元，则租出床位减少10张，若每床每日收费再提高2元，则租出床位再减少10张，以每提高2元的这种变化方法变化下去，每床每日提高元可获最大利润。
11. 校运动会小明参加铅球比赛，若某次投掷，铅球飞行的高度y（米）与水平距离x（米）之间的函数关系式为 ，那么小明这次投掷的成绩是米．
12. 2013年5月26日，中国羽毛球队蝉联苏迪曼杯团体赛冠军，成就了首个五连冠霸业．比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图)，若不考虑外力因素，羽毛球行进高度y(米)与水平距离x(米)之间满足关系y＝－ x2＋ x＋ ，则羽毛球飞出的水平距离为米．
13. 某圆形喷水池的水柱如图①所示，如果曲线APB表示落点B离点O最远的一条水流，如图②所示，其上的水珠的高度y(米)关于水平距离x(米)的函数解析式为y=－x2＋4x＋ ，那么圆形水池的半径至少为米时，才能使喷出的水流不落在水池外．
14. 数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：售价（元/件）
100
110
120
130
…
月销量（件）
200
180
160
140
…
已知该运动服的进价为每件60元，设售价为x（x≥100）元，则月销量是件，销售该运动服的月利润为元（用含x的式子表示）.
15. 两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A，E，F在同一直线上.跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E，F. 若点B和点E、点C和F的离地高度分别相同，现消防员将水流抛物线向上平移0.4m，再向左后退了m，恰好把水喷到F处进行灭火．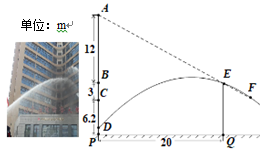
三、解答题
-
16. 小明在一次打篮球时，篮球传出后的运动路线为如图所示的抛物线，以小明所站立的位置为原点O建立平面直角坐标系，篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=- x2+x+c.
(1)、求y与x之间的函数表达式；
(2)、球在运动的过程中离地面的最大高度；(3)、小亮手举过头顶，跳起后的最大高度为BC=2.5m，若小亮要在篮球下落过程中接到球，求小亮离小明的最短距离OB.
17. 足球比赛中，某运动员将在地面上的足球对着球门踢出，图中的抛物线是足球的飞行高度y（m）关于飞行时间x（s）的函数图象（不考虑其它因素），已知足球飞出1s时，足球的飞行高度是2.44m，足球从飞出到落地共用3s．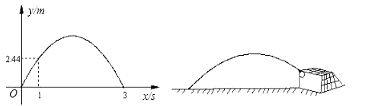
(1)、求y关于x的函数解析式；
(2)、足球的飞行高度能否达到4.88 m？请说明理由；(3)、假设没有拦挡，足球将擦着球门左上角射入球门，球门的高为2.44 m（如图所示，足球的大小忽略不计）．如果为了能及时将足球扑出，那么足球被踢出时，离球门左边框12m处的守门员至少要在几s内到球门的左边框？
18. 某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，井建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数P= （0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：Q=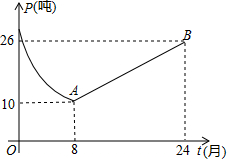
(1)、当8＜t≤24时，求P关于t的函数解析式；
(2)、设第t个月销售该原料药的月毛利润为w（单位：万元）①求w关于t的函数解析式；
②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P的最小值和最大值．
19. “绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的50%标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．
(1)、求该型号自行车的进价和标价分别是多少元？
(2)、若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？
20. 某广场喷泉的喷嘴安装在平地上．有一喷嘴喷出的水流呈抛物线状，喷出的水流高度y（m）与喷出水流喷嘴的水平距离x（m）之间满足
(1)、喷嘴能喷出水流的最大高度是多少？(2)、喷嘴喷出水流的最远距离为多少？
21. 某公司销售某一种新型通讯产品，已知每件产品的进价为4万元，每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现，月销售量y(件)与销售单价x (万元)之间存在着如图所示的一次函数关系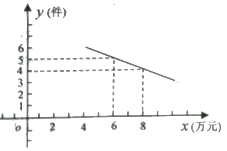
(1)、求y关于x的函数关系式(直接写出结果)
(2)、试写出该公司销售该种产品的月获利z(万元)关于销售单价x(万元)的函数关系式、当销售单价x为何值时，月获利最大?并求这个最大值(月获利一月销售额一月销售产品总进价一月总开支，)
(3)、若公司希望该产品一个月的销售获利不低于5万元，借助(2)中函数的图象，请你帮助该公司确定销售单价的范围.在此情况下，要使产品销售量最大，你认为销售单价应定为多少万元