2018-2019学年数学人教版九年级上册22.2.2 图象法求一元二次方程的近似根同步训练

试卷更新日期：2018-08-21 类型：同步测试

进入出卷网下载

一、选择题

1. 根据下列表格对应值：
x
3.24
3.25
3.26
ax²+bx+c
-0.02
0.01
0.03
判断关于x的方程ax²+bx+c=0 $(a \neq 0)$ 的一个解x的范围是（）

A、x＜3.24 B、3.24＜x＜3.25 C、3.25＜x＜3.26 D、3.25＜x＜3.28

查看试题解析
2. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴是直线x=﹣1及部分图像（如图所示），由图像可知关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两个根分别是 $x_{1} = 1.3$ 和 $x_{2} =$ （）

A、﹣1.3 B、﹣2.3 C、﹣3.3 D、﹣4.3

查看试题解析
3. 二次函数 $y = x^{2} - 2 x - 3$ 的图象如图所示．当y＜0时，自变量x的取值范围是（）．

A、－1＜x＜3 B、x＜－1 C、x＞3 D、x＜－1或x＞3

查看试题解析
4. 如图是二次函数y=ax²+bx+c的部分图象，由图象可知不等式ax²+bx+c>0的解集是（）.

A、 $- 1 < x < 5$ B、 $x > 5$ C、 $x 〈 - 1 且 x 〉 5$ D、 $x 〈 - 1 或 x 〉 5$

查看试题解析
5. 小明利用二次函数的图象估计方程x²－2x－2＝0的近似解，如表是小明探究过程中的一些计算数据．根据表中数据可知，方程x²－2x－2＝0必有一个实数根在（）
x
1.5
2
2.5
3
3.5
x²－2x－2
－2.75
－2
－0.75
1
3.25

A、1.5和2之间 B、2和2.5之间 C、2.5和3之间 D、3和3.5之间

查看试题解析
6. 根据抛物线y＝x²＋3x－1与x轴的交点的坐标，可以求出下列方程中哪个方程的近似解（）

A、x²＋3x－1＝0 B、x²＋3x＋1＝0 C、3x²＋x－1＝0 D、x²－3x＋1＝（）

查看试题解析
7. 已知二次函数y＝x²－2x＋m(m为常数)的图象与x轴的一个交点为(－1，0)，则关于x的一元二次方程x²－2x＋m＝0的两个实数根是（）

A、x₁＝1，x₂＝2 B、x₁＝1，x₂＝3 C、x₁＝－1，x₂＝2 D、x₁＝－1，x₂＝3

查看试题解析
8. 二次函数y=ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c=0；③若方程a（x+5）（x﹣1）=﹣1有两个根x₁和x₂ ，且x₁＜x₂ ，则﹣5＜x₁＜x₂＜1；④若方程|ax²+bx+c|=1有四个根，则这四个根的和为﹣4．其中正确的结论有（）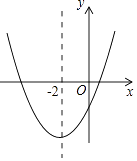

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 二次函数y＝x²＋ax＋a与x轴的交点分别是A(x₁ ， 0)、B(x₂ ， 0)，且x₁＋x₂－x₁x₂＝－10，则抛物线的顶点坐标是．

查看试题解析
10. 如图，抛物线 $y = a x^{2}$ 与直线 $y = b x + c$ 的两个交点坐标分别为 $A (- 2 ， 4)$ ， $B (1 ， 1)$ ，则方程 $a x^{2} = b x + c$ 的解是．

查看试题解析
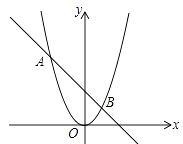11. 已知：二次函数y=ax²+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示，那么它的图象与x轴的另一个交点坐标是．
x
…
﹣1
0
1
2
…
y
…
0
3
4
3
…

查看试题解析
12. 若二次函数y＝x²＋3x－c(c为整数)的图象与x轴没有交点，则c的最大值是.

查看试题解析
13. $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标（-1，-3.2）及部分图象（如图所示），由图象可知关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两个根分别是x₁=1.3和x₂= ．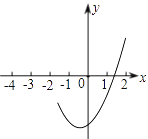

查看试题解析
14. 已知关于x的方程x²+2kx+k²+k+3=0的两根分别是x₁、x₂ ，则（x₁﹣1）²+（x₂﹣1）²的最小值是

查看试题解析
15. 若关于x的一元二次方程a(x＋m)²－3＝0的两个实数根分别为x₁＝－1，x₂＝3，则抛物线y＝a(x＋m－2)²－3与x轴的交点坐标为．

查看试题解析

三、解答题

16. 已知抛物线 $y = a x^{2} + b x - 8 (a \neq 0)$ 的对称轴是直线 $x = 1$ ，

(1)、求证： $2 a + b = 0$ ；

(2)、若关于x的方程 $a x^{2} + b x - 8 = 0$ ，有一个根为4，求方程的另一个根．

查看试题解析
17. 抛物线 $y = - x^{2} + (m - 1) x + m$ 与y轴交于点 $(0 ， 3)$ ．

(1)、求抛物线的解析式；

(2)、求抛物线与坐标轴的交点坐标；

(3)、①当x取什么值时， $y > 0$ ？ $②$ 当x取什么值时，y的值随x的增大而减小？

查看试题解析
18. 抛物线 $y = a x^{2} + 2 x + c$ 经过点 $B (3 ， 0)$ 、 $C (0 ， 3)$ 两点．

(1)、求抛物线顶点D的坐标；

(2)、抛物线与x轴的另一交点为A ，求 $△ A B C$ 的面积．

查看试题解析
19. 已知二次函数y=﹣ $\frac{3}{16}$ x²+bx+c的图象经过A（0，3），B（﹣4，﹣ $\frac{9}{2}$ ）两点．

(1)、求b，c的值．

(2)、二次函数y=﹣ $\frac{3}{16}$ x²+bx+c的图象与x轴是否有公共点，求公共点的坐标；若没有，请说明情况．

查看试题解析
20. 二次函数y=ax²＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题．

(1)、写出方程ax²＋bx＋c＝0的两个根；

(2)、写出不等式ax²＋bx＋c＞0的解集；

(3)、写出y随x的增大而减小的自变量x的取值范围；

(4)、若方程ax²＋bx＋c＝k有两个不相等的实数根，求k的取值范围．

查看试题解析
21. 根据下列要求，解答相关问题．

(1)、请补全以下求不等式 $x^{2} - 2 x < 0$ 的解集的过程：
①构造函数，画出图象：根据不等式特征构造二次函数y= $x^{2} - 2 x$ ；并在下面的坐标系中（图1）画出二次函数y= $x^{2} - 2 x$ 的图象（只画出大致图象即可）；
②求得界点，标示所需：当 $y = 0$ 时，求得方程 $x^{2} - 2 x = 0$ 的解为；并用虚线标示出函数y= $x^{2} - 2 x$ 图象中 $y$ ＜0的部分；
③借助图象，写出解集：由所标示图象，可得不等式 $x^{2} - 2 x$ ＜0的解集为．

(2)、请你利用上面求不等式解集的过程，求不等式 $x^{2} - 2 x$ -3≥0的解集．

查看试题解析

x	3.24	3.25	3.26
ax²+bx+c	-0.02	0.01	0.03

x	1.5	2	2.5	3	3.5
x²－2x－2	－2.75	－2	－0.75	1	3.25

x	…	﹣1	0	1	2	…
y	…	0	3	4	3	…

2018-2019学年数学人教版九年级上册22.2.2 图象法求一元二次方程的近似根 同步训练

一、选择题

二、填空题

三、解答题

2018-2019学年数学人教版九年级上册22.2.2 图象法求一元二次方程的近似根同步训练