2018-2019学年数学人教版九年级上册 第22章 二次函数 单元检测b卷
试卷更新日期:2018-08-21 类型:单元试卷
一、2018-2019学年数学人教版九年级上册 第22章 二次函数 单元检测b卷 一 、选择题
-
1. 若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则符合条件的点P( )
A、有且只有1个 B、有且只有2个 C、有且只有3个 D、有无穷多个2. 在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )A、a≤﹣1或 ≤a< B、 ≤a< C、a≤ 或a> D、a≤﹣1或a≥3. 抛物线y=ax2+bx+c(a≠0)图象如图所示,下列结论错误的是( )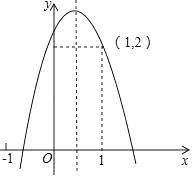 A、abc<0 B、a+c<b C、b2+8a>4ac D、2a+b>04. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-1,则 的值为( )
A、abc<0 B、a+c<b C、b2+8a>4ac D、2a+b>04. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-1,则 的值为( )
A、3或6 B、1或6 C、1或3 D、4或65. 若抛物线 与 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线 ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A、 B、 C、 D、6. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )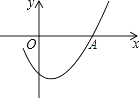 A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=07. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、
A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=07. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、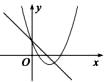 B、
B、 C、
C、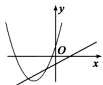 D、
D、 8. 若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线。已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A、(-3,-6) B、(-3,0) C、(-3,-5) D、(-3,-1)9. 若二次函数 的图象经过点(2,0),且其对称轴为 ,则使函数值 成立的 的取值范围是( )A、 或 B、 ≤ ≤ C、 ≤ 或 ≥ D、10. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A.B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.其中正确的有( )
8. 若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线。已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A、(-3,-6) B、(-3,0) C、(-3,-5) D、(-3,-1)9. 若二次函数 的图象经过点(2,0),且其对称轴为 ,则使函数值 成立的 的取值范围是( )A、 或 B、 ≤ ≤ C、 ≤ 或 ≥ D、10. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A.B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.其中正确的有( )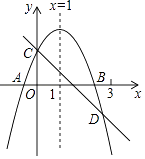 A、4个 B、3个 C、2个 D、1个11. 如图,抛物线y=﹣ x2+ x+ 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
A、4个 B、3个 C、2个 D、1个11. 如图,抛物线y=﹣ x2+ x+ 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( ) A、(4,3) B、(5, ) C、(4, ) D、(5,3)12. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
A、(4,3) B、(5, ) C、(4, ) D、(5,3)12. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )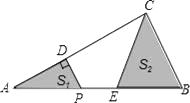 A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小13. 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有 .
A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小13. 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有 .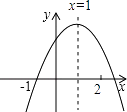 14. 如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为 .
14. 如图,正方形EFGH的顶点在边长为2的正方形的边上.若设AE=x,正方形EFGH的面积为y,则y与x的函数关系为 .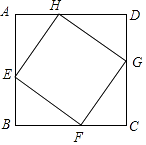 15. 已知当x1=a,x2=b,x3=c时,二次函数y= x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
15. 已知当x1=a,x2=b,x3=c时,二次函数y= x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
16. 某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为 .
17. 二次函数y=x2﹣2x﹣3的图象如图所示,若线段AB在x轴上,且AB为2 个单位长度,以AB为边作等边△ABC,使点C落在该函数y轴左侧的图象上,则点C的坐标为 .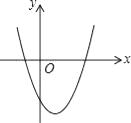 18. 如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 .
18. 如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 .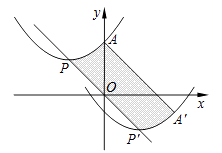 19. 已知二次函数y=﹣ x2+bx+c的图象经过A(0,3),B(﹣4,﹣ )两点.(1)、求b,c的值.
19. 已知二次函数y=﹣ x2+bx+c的图象经过A(0,3),B(﹣4,﹣ )两点.(1)、求b,c的值.
(2)、二次函数y=﹣ x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.20. 已知二次函数y=2(x﹣1)(x﹣m﹣3)(m为常数).(1)、求证:不论m为何值,该函数的图象与x轴总有公共点;
(2)、当m取什么值时,该函数的图象与y轴的交点在x轴的上方?
21. 绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.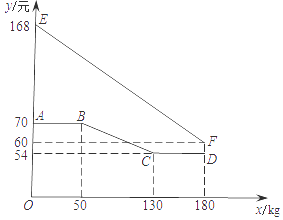 (1)、求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(1)、求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)、直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)、当产量为多少时,这种产品获得的利润最大?最大利润为多少?
22. 如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D. (1)、求线段AD的长;
(1)、求线段AD的长;
(2)、平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.23. 某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系关于销售单价,日销售量,日销售利润的几组对应值如表:销售单价x(元)
85
95
105
115
日销售量y(个)
175
125
75
m
日销售利润w(元)
875
1875
1875
875
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)、求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)、根据以上信息,填空:该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;
(3)、公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
24. 平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点. (1)、当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(1)、当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)、过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;(3)、在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.25. 如图,已知抛物线y=ax2+bx与x轴分别交于原点O和点F(10,0),与对称轴l交于点E(5,5).矩形ABCD的边AB在x轴正半轴上,且AB=1,边AD,BC与抛物线分别交于点M,N.当矩形ABCD沿x轴正方向平移,点M,N位于对称轴l的同侧时,连接MN,此时,四边形ABNM的面积记为S;点M,N位于对称轴l的两侧时,连接EM,EN,此时五边形ABNEM的面积记为S.将点A与点O重合的位置作为矩形ABCD平移的起点,设矩形ABCD平移的长度为t(0≤t≤5)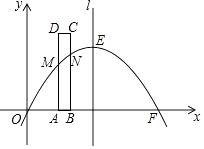 (1)、求出这条抛物线的表达式;
(1)、求出这条抛物线的表达式;
(2)、当t=0时,求S△OBN的值;
(3)、当矩形ABCD沿着x轴的正方向平移时,求S关于t(0<t≤5)的函数表达式,并求出t为何值时S有最大值,最大值是多少?26. 如图,已知抛物线交x轴于A.B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.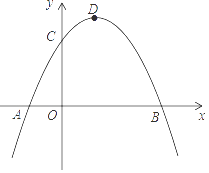 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;(3)、若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.