2018-2019学年数学人教版九年级上册第22章二次函数单元检测a卷

试卷更新日期：2018-08-21 类型：单元试卷

进入出卷网下载

一、选择题

1. 抛物线y=﹣ $\frac{3}{5}$ （x+ $\frac{1}{2}$ ）²﹣3的顶点坐标是（）

A、（ $\frac{1}{2}$ ，﹣3） B、（﹣ $\frac{1}{2}$ ，﹣3） C、（ $\frac{1}{2}$ ，3） D、（﹣ $\frac{1}{2}$ ，3）

查看试题解析
2. 抛物线y=（x﹣2）²﹣1可以由抛物线y=x²平移而得到，下列平移正确的是（）

A、先向左平移2个单位长度，然后向上平移1个单位长度 B、先向左平移2个单位长度，然后向下平移1个单位长度 C、先向右平移2个单位长度，然后向上平移1个单位长度 D、先向右平移2个单位长度，然后向下平移1个单位长度

查看试题解析
3. 将抛物线y=﹣5x²+1向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线为（）

A、y=﹣5（x+1）²﹣1 B、y=﹣5（x﹣1）²﹣1 C、y=﹣5（x+1）²+3 D、y=﹣5（x﹣1）²+3

查看试题解析
4. 已知二次函数 $y = x^{2} - x + \frac{1}{4} m - 1$ 的图象与x轴有交点，则m的取值范围是（）

A、 $m \leq 5$ B、 $m \geq 2$ C、 $m < 5$ D、 $m > 2$

查看试题解析
5. 如图，二次函数 $y = a x^{2} + b x$ 的图象开口向下，且经过第三象限的点p若点P的横坐标为-1，则一次函数 $y = (a - b) x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 已知二次函数y=x²﹣2mx（m为常数），当﹣1≤x≤2时，函数值y的最小值为﹣2，则m的值是（）

A、 $\frac{3}{2}$ B、 $\sqrt{2}$ C、 $\frac{3}{2}$ 或 $\sqrt{2}$ D、 $- \frac{3}{2}$ 或 $\sqrt{2}$

查看试题解析
7. 已知抛物线y=ax²（a＞0）过A（﹣2，y₁）、B（1，y₂）两点，则下列关系式一定正确的是（）

A、y₁＞0＞y₂ B、y₂＞0＞y₁ C、y₁＞y₂＞0 D、y₂＞y₁＞0

查看试题解析
8. 若二次函数y=ax²+1的图象经过点（﹣2，0），则关于x的方程a（x﹣2）²+1=0的实数根为（）

A、x₁=0，x₂=4 B、x₁=﹣2，x₂=6 C、x₁= $\frac{3}{2}$ ，x₂= $\frac{5}{2}$ D、x₁=﹣4，x₂=0

查看试题解析
9. 如图，在△ABC中，∠C=90°，AB=10cm，BC=8cm，点P从点A沿AC向点C以1cm/s的速度运动，同时点Q从点C沿CB向点B以2cm/s的速度运动（点Q运动到点B停止），在运动过程中，四边形PABQ的面积最小值为（）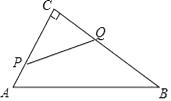

A、19cm² B、16cm² C、15cm² D、12cm²

查看试题解析
10. 已知二次函数，当x＞0时，y随x的增大而（填“增大”或“减小”）

查看试题解析
11. 抛物线y=2（x+2）²+4的顶点坐标为．

查看试题解析
12. 已知：二次函数 $y = a x^{2} + b x + c$ 图象上部分点的横坐标x与纵坐标y的对应值如表格所示，那么它的图象与x轴的另一个交点坐标是．
x

-1
0
1
2

y

0
3
4
3


查看试题解析
13. 右图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加m。

查看试题解析
14. 如图，直线y=mx+n与抛物线y=ax²+bx+c交于A（﹣1，p），B（4，q）两点，则关于x的不等式mx+n＞ax²+bx+c的解集是．

查看试题解析
15. 已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是．

查看试题解析

二、解答题

16. 已知抛物线y=ax²+bx﹣3（a≠0）经过点（﹣1，0），（3，0），求a，b的值．

查看试题解析
17. 某商品的进价为每件40元，售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．设每件商品的售价为x元（x为正整数），每个月的销售利润为y元．

(1)、当每件商品的售价是多少元时，每个月的利润刚好是2250元？

(2)、当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

查看试题解析
18. 2016年12月29日至31日，黔南州第十届旅游产业发展大会在“中国长寿之乡”﹣﹣罗甸县举行，从中寻找到商机的人不断涌现，促成了罗甸农民工返乡创业热潮．某“火龙果”经营户有A．B两种“火龙果”促销，若买2件A种“火龙果”和1件B种“火龙果”，共需120元；若买3件A种“火龙果”和2件B种“火龙果”，共需205元．

(1)、设A，B两种“火龙果”每件售价分别为a元、b元，求a、b的值；

(2)、B种“火龙果”每件的成本是40元，根据市场调查：若按（1）中求出的单价销售，该“火龙果”经营户每天销售B种“火龙果”100件；若销售单价每上涨1元，B种“火龙果”每天的销售量就减少5件．
①求每天B种“火龙果”的销售利润y（元）与销售单价x（元）之间的函数关系？
②求销售单价为多少元时，B种“火龙果”每天的销售利润最大，最大利润是多少？

查看试题解析
19. 某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价．现在的售价为每箱36元，每月可销售60箱．市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元（x为正整数），每月的销量为y箱．

(1)、写出y与x中间的函数关系式和自变量x的取值范围；

(2)、超市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？

查看试题解析
20. 如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

(1)、若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
21. “五一”期间，恒大影城隆重开业，影城每天运营成本为1000元，试营业期间统计发现，影城每天售出的电影票张数y（张）与电影票售价x（元/张）之间满足一次函数关系：y=﹣4x+220（10≤x≤50，且x是整数），设影城每天的利润为w（元）（利润=票房收入﹣运营成本）．

(1)、试求w与x之间的函数关系式；

(2)、影城将电影票售价定为多少元/张时，每天获利最大？最大利润是多少元？

查看试题解析
22. 工人师傅用一块长为10dm，宽为6dm的矩形铁皮制作一个无盖的长方体容器，需要将四角各裁掉一个正方形．（厚度不计）

(1)、在图中画出裁剪示意图，用实线表示裁剪线，虚线表示折痕；并求长方体底面面积为12dm²时，裁掉的正方形边长多大？

(2)、若要求制作的长方体的底面长不大于底面宽的五倍，并将容器进行防锈处理，侧面每平方分米的费用为0.5元，底面每平方分米的费用为2元，裁掉的正方形边长多大时，总费用最低，最低为多少？

查看试题解析
23. 某商店经销一种双肩包，已知这种双肩包的成本价为每个30元．市场调查发现，这种双肩包每天的销售量y（单位：个）与销售单价x（单位：元）有如下关系：y=﹣x+60（30≤x≤60）．
设这种双肩包每天的销售利润为w元．

(1)、求w与x之间的函数解析式；

(2)、这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？

(3)、如果物价部门规定这种双肩包的销售单价不高于48元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元？

查看试题解析

2018-2019学年数学人教版九年级上册 第22章 二次函数 单元检测a卷

一、选择题

二、解答题

2018-2019学年数学人教版九年级上册第22章二次函数单元检测a卷