2016-2017学年浙江省杭州市萧山区临浦片八年级上学期期中数学试卷
试卷更新日期:2017-02-23 类型:期中考试
一、选择题
-
1. 下列图案中,是轴对称图形的有( )个.
 A、1 B、2 C、3 D、42. 下列语句是命题的是( )A、作直线AB的垂线 B、在线段AB上取点C C、同旁内角互补 D、垂线段最短吗?3. 已知等腰△两条边的长分别是3和6,则它的周长是( )A、12 B、15 C、12或15 D、15或184. 如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A、1 B、2 C、3 D、42. 下列语句是命题的是( )A、作直线AB的垂线 B、在线段AB上取点C C、同旁内角互补 D、垂线段最短吗?3. 已知等腰△两条边的长分别是3和6,则它的周长是( )A、12 B、15 C、12或15 D、15或184. 如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( ) A、SSS B、ASA C、SSA D、HL5. 若a<b,则下列各式中一定成立的是( )A、a﹣1<b﹣1 B、 > C、﹣a<﹣b D、ac<bc6. 下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( )A、5 B、2 C、4 D、87. 如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )
A、SSS B、ASA C、SSA D、HL5. 若a<b,则下列各式中一定成立的是( )A、a﹣1<b﹣1 B、 > C、﹣a<﹣b D、ac<bc6. 下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( )A、5 B、2 C、4 D、87. 如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( ) A、P为∠A,∠B两角平分线的交点 B、P为AC,AB两边上的高的交点 C、P为∠A的角平分线与AB的垂直平分线的交点 D、P为AC,AB两边的垂直平分线的交点8. 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,
A、P为∠A,∠B两角平分线的交点 B、P为AC,AB两边上的高的交点 C、P为∠A的角平分线与AB的垂直平分线的交点 D、P为AC,AB两边的垂直平分线的交点8. 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:
①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.
其中正确的结论为( )
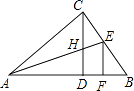 A、①②④ B、①②③ C、②③ D、①③9. △ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )A、4.8 B、4.8或3.8 C、3.8 D、510.
A、①②④ B、①②③ C、②③ D、①③9. △ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )A、4.8 B、4.8或3.8 C、3.8 D、510.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 等腰三角形的一个外角等于130°,则顶角是12. 写出“对顶角相等”的逆命题 .13. 在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=4,则点D到斜边AB的距离为 .
 14. 不等式组 有3个整数解,则m的取值范围是 .15. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
14. 不等式组 有3个整数解,则m的取值范围是 .15. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1 , 得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2 , 得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3 , 得第3条线段A2A3;…
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=
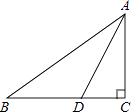
 16. 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 .
16. 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 .
三、解答题
-
17. 解不等式 ,并把它的解集在数轴上表示出来.
 18. 如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.
18. 如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.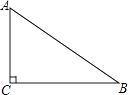 (1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=37°,求∠CAD的度数.19. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
(1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=37°,求∠CAD的度数.19. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
 20. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
20. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.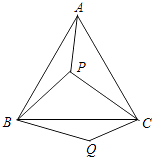 (1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.21. 阅读下列材料:
(1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.21. 阅读下列材料:解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组 的解都为非负数.
(1)、求a的取值范围;(2)、已知2a﹣b=1,且,求a+b的取值范围;(3)、已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)22. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒. (1)、出发2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为直角三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
(1)、出发2秒后,求△ABP的周长.(2)、问t满足什么条件时,△BCP为直角三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?