2015-2016学年浙江省温州市洞头县六校联考八年级下学期期中数学试卷

试卷更新日期：2017-02-23 类型：期中考试

进入出卷网下载

一、选择题

1. 二次根式 $\sqrt{x - 1}$ 中字母x的取值范围是（）

A、x＜1 B、x≥1 C、x≤0 D、x≥0

查看试题解析
2. 如图中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如果一个多边形的内角和是720°，那么这个多边形是（）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
4. 下列方程是一元二次方程的是（）

A、2xy﹣7=0 B、x²﹣7=0 C、﹣7x=0 D、5（x+1）=7²

查看试题解析
5. 在▱ABCD中，∠A：∠B：∠C=1：2：1，则∠D等于（）

A、0° B、60° C、120° D、150°

查看试题解析
6. 若点P（a，2）与Q（﹣1，b）关于坐标原点对称，则a，b分别为（）

A、﹣1，2 B、1，﹣2 C、1，2 D、﹣1，﹣2

查看试题解析
7. 下列计算正确的是（）

A、 $\sqrt{3}$ + $\sqrt{2}$ = $\sqrt{5}$ B、 $\sqrt{8}$ ﹣ $\sqrt{2}$ = $\sqrt{6}$ C、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{6}$ D、 $\sqrt{8} \div \sqrt{2}$ =4

查看试题解析
8. 为了参加市中学生篮球运动会，一支校篮球队准备购买双运动鞋，各种尺码的统计如表所示，则这双运动鞋尺码的众数和中位数分别为（）
尺码（厘米）
25
25.5
26
26.5
27
购买量（双）
1
4
2
1
1

A、25.5cm 26 cm B、26 cm 25.5 cm C、25.5 cm 25.5 cm D、26 cm 26 cm

查看试题解析
9. 如果1≤a≤ $\sqrt{2}$ ，则 $\sqrt{a^{2} - 2 a + 1} + | a - 2 |$ 的值是（）

A、6+a B、﹣6﹣a C、﹣a D、1

查看试题解析
10. 某校去年投资2万元购买实验器材，预期明年的投资额为8万元．若该校这两年购买实验器材的投资的年平均增长率为x，则下面所列方程正确的是（）

A、2（1+2x）=8 B、2（1+x）²=8 C、8（1﹣2x）=2 D、8（1﹣x）²=2

查看试题解析

二、填空题

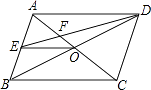
11. 当x=﹣2时，二次根式 $\sqrt{2 - 7 x}$ 的值是．

查看试题解析
12. 平行四边形ABCD的周长为30 cm，AB：BC=2：3，则AB= ．

查看试题解析
13. 一元二次方程x²=3x的解是：．

查看试题解析
14. 已知平行四边形ABCD中，AC，BD交于点O，若AB=6，AC=8，则BD的取值范围是

查看试题解析
15. 有一组数据：3，a，4，6，7．它们的平均数是5，那么这组数据的方差是．

查看试题解析
16. 已知一个一元二次方程的一个根为2，且常数项为0，则这个一元二次方程可以是．（只需写出一个方程即可）

查看试题解析
17. 若方程kx²﹣9x+8=0的一个根为1，则另一个根为

查看试题解析
18. 如图，O为▱ABCD的对角线交点，E为AB的中点，DE交AC于点F，若S_四边形_ABCD=12，则S_△_BOE的值为．

查看试题解析

三、解答题

19. 计算与解方程

(1)、计算：（﹣ $\sqrt{5}$ ）²+（ $\sqrt{2}$ +1）（ $\sqrt{2}$ ﹣1）﹣ $\sqrt{\frac{2}{3}}$ × $\sqrt{1 \frac{1}{2}}$

(2)、解方程：x²﹣2x﹣1=0．

查看试题解析
20. 如图，在5×5的正方形网格中，每个小正方形的边长为1，请在所给网格中按下列要求画出图形．

(1)、（i）已知点A在格点（即小正方形的顶点）上，画一条线段AB，长度为 $\sqrt{10}$ ，且点B在格点上．
（ii）以上题所画的线段AB为一边，另外两条边长分别为 $\sqrt{5}$ ， $\sqrt{13}$ ．画一个△ABC，使点C在格点上（只需画出符合条件的一个三角形）．

(2)、所画出的△ABC的边AB上的高线长为．（直接写出答案）

查看试题解析
21. 某政府部门进行公务员招聘考试，其中三人中录取一人，他们的成绩如下：
人
测试成绩
题目
甲
乙
丙
文化课知识
74
87
69
面试
58
74
70
平时表现
87
43
65

(1)、按照平均成绩甲、乙、丙谁应被录取？

(2)、若按照文化课知识、面试、平时表现的成绩已4：3：1的比例录取，甲、乙、丙谁应被录取？

查看试题解析
22. 如图，在▱ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．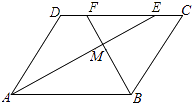

(1)、试说明：AE⊥BF；

(2)、判断线段DF与CE的大小关系，并予以说明．

查看试题解析
23. 某超市销售一种饮料，平均每天可售出100箱，每箱利润120元．为了扩大销售，增加利润，超市准备适当降价．据测算，若每箱每降低1元，每天可多售出2箱．

(1)、如果要使每天销售饮料获利14000元，问每箱应降价多少元？

(2)、试问当降价几元时，总利润达到最大值？

查看试题解析
24.
如图，已知A，B两点是直线AB与x轴的正半轴，y轴的正半轴的交点，且OA，OB的长分别是x²﹣14x+48=0的两个根（OA＞OB），射线BC平分∠ABO交x轴于C点，若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动，运动时间为t秒．

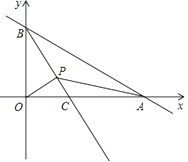(1)、求OA，OB的长；

(2)、设△APB和△OPB的面积分别为s₁ ， s₂ ，求s₁：s₂；

(3)、在点P的运动过程中，△OPB可能是等腰三角形吗？若可能，直接写出时间t；若不可能，请说明理由．

查看试题解析

人	测试成绩
题目	甲	乙	丙
文化课知识	74	87	69
面试	58	74	70
平时表现	87	43	65

尺码（厘米）	25	25.5	26	26.5	27
购买量（双）	1	4	2	1	1