2018-2019学年数学北师大版九年级上册第1章 特殊的平行四边形 单元检测a卷
试卷更新日期:2018-08-17 类型:单元试卷
一、选择题
-
1. 正方形具备而菱形不具备的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、每条对角线平分一组对角2. 已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A、4个 B、3个 C、2个 D、1个3. 相邻两边长分别为2和3的平行四边形,若边长保持不变,其内角大小变化,则它可以变为( )A、矩形 B、菱形 C、正方形 D、矩形或菱形4. 如图,在▱ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF,则四边形AECF是( ) A、矩形 B、菱形 C、正方形 D、无法确定5. 如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A、矩形 B、菱形 C、正方形 D、无法确定5. 如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( ) A、邻边相等的矩形是正方形 B、对角线相等的菱形是正方形 C、两个全等的直角三角形构成正方形 D、轴对称图形是正方形6. 如图,已知▱ABCD中,AE⊥BC,AF⊥DC,BC∶CD= 3∶2,AB=EC,则∠EAF=( )
A、邻边相等的矩形是正方形 B、对角线相等的菱形是正方形 C、两个全等的直角三角形构成正方形 D、轴对称图形是正方形6. 如图,已知▱ABCD中,AE⊥BC,AF⊥DC,BC∶CD= 3∶2,AB=EC,则∠EAF=( ) A、 B、 C、 D、7. 下列命题正确的是( )A、对角线互相平分的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8. 如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A、 B、 C、 D、7. 下列命题正确的是( )A、对角线互相平分的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8. 如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( ) A、AB=BC B、AC=BC C、∠B=60° D、∠ACB=60°9. 如图,在▱ABCD中,对角线 相交于点O,添加下列条件不能判定▱ABCD是菱形的只有( )
A、AB=BC B、AC=BC C、∠B=60° D、∠ACB=60°9. 如图,在▱ABCD中,对角线 相交于点O,添加下列条件不能判定▱ABCD是菱形的只有( ) A、 B、 C、 D、10. 如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积为( )
A、 B、 C、 D、10. 如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积为( ) A、 B、 C、 D、11. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
A、 B、 C、 D、11. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( ) A、
A、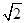 B、2
B、2 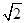 C、2
D、1
12.
C、2
D、1
12.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 A、50° B、60° C、70° D、80°
A、50° B、60° C、70° D、80°二、填空题
-
13. 如图,已知四边形ABCD是菱形,∠A=72°,将它分割成如图所示的四个等腰三角形,那么∠1+∠2+∠3= .
 14. 如图,矩形ABCD内有一点E,连接AE,DE,CE,使AD=ED=EC,若∠ADE=20°,则∠AEC=.
14. 如图,矩形ABCD内有一点E,连接AE,DE,CE,使AD=ED=EC,若∠ADE=20°,则∠AEC=. 15. 如图,两条笔直的公路l₁、l₂相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D.已知AB=BC=CD=DA=5 km,村庄C到公路l₁的距离为4 km,则村庄C到公路l₂的距离是km.
15. 如图,两条笔直的公路l₁、l₂相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D.已知AB=BC=CD=DA=5 km,村庄C到公路l₁的距离为4 km,则村庄C到公路l₂的距离是km. 16. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连结DE,则DE的最小值为 .
16. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连结DE,则DE的最小值为 .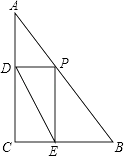 17. 如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为 .
17. 如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为 .
三、解答题
-
18. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,点P是AC的中点.求证:∠BDP=∠DBP.
 19. 如图,▱ABCD中,AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其它条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程(要求:推理过程中要用到“平行四边形”和“角平分线”这两个条件).
19. 如图,▱ABCD中,AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN交于P,CN与DQ交于M,在不添加其它条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程(要求:推理过程中要用到“平行四边形”和“角平分线”这两个条件).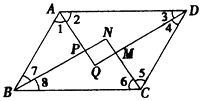 20. 如图,在梯形 中, 两点在边 上,且四边形 是平行四边形.
20. 如图,在梯形 中, 两点在边 上,且四边形 是平行四边形. (1)、 与 有何等量关系?请说明理由;
(1)、 与 有何等量关系?请说明理由;
(2)、当 时,求证:平行四边形 是矩形.21. 如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠BAO=∠DAO. (1)、求证:平行四边形ABCD是菱形;
(1)、求证:平行四边形ABCD是菱形;
(2)、请添加一个条件使菱形ABCD为正方形.22. 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF. (1)、求证:四边形ADCF是平行四边形;(2)、当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
(1)、求证:四边形ADCF是平行四边形;(2)、当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.

