2018-2019学年数学北师大版九年级上册1.2 矩形的性质与判定（3） 同步训练
试卷更新日期：2018-08-17 类型：同步测试
一、选择题
-
1. 如图，在矩形ABCD中，对角线
相交于点 
，则AB的长是（ ）
A、3cm B、6cm C、10cm D、12cm2. 如图，点O是矩形ABCD的对角线AC的中点，OM//AB交AD于点M，若OM=3，BC=10，则OB的长为（ ）
A、5 B、4 C、 D、3. 如图，将长方形ABCD沿直线BD折叠，使点C落在点E处，BE交AD于F，连接CE，下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD，正确的是（ ）
A、①② B、①②③ C、②③④ D、①②③④4. 如图，在矩形ABCD中，AB＝2，BC＝3，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为（ ）
A、2 B、 C、3 D、5. 如图，E，F分别是矩形ABCD的边AD、AB上的点，若EF=EC，EF⊥EC，DC=
，则BE的长为（ ）
A、
B、
C、4
D、2
6.如图，矩形ABCD的两条对角线相交于点O，∠AOB＝120°，AD＝2，点E是BC的中点，连结OE，则OE的长是（ ）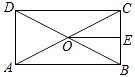
A、 B、2 C、2 D、47. 如图，△ABC中，∠ABC＝∠BAC，D是AB的中点，EC∥AB，DE∥BC，AC与DE交于点O．下列结论中，不一定成立的是（ ）
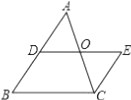A、AC＝DE B、AB＝AC C、AD＝EC D、OA＝OE8.如图，E是矩形ABCD内的一个动点，连接EA、EB、EC、ED，得到△EAB、△EBC、△ECD、△EDA，设它们的面积分别是m、n、p、q，给出如下结论：
①m+n=q+p；
②m+p=n+q；
③若m=n，则E点一定是AC与BD的交点；
④若m=n，则E点一定在BD上．
其中正确结论的序号是（ ）
A、①③ B、②④ C、①②③ D、②③④9. 如图，E，F分别是矩形ABCD边AD，BC上的点，且△ABG，△DCH的面积分别为15和20，则图中阴影部分的面积为（ ）
A、15 B、20 C、35 D、4010. 如图，在 中， 是 的中点，将 沿 翻折得到 ，连接 ，则线段 的长等于（ ）
A、2 B、 C、 D、二、填空题
-
11. 在矩形ABCD中，AB＝2，BC＝3，若点E为边CD的中点，连接AE，过点B作BF⊥AE于点F，则BF长为.
12. 如图，点E是矩形ABCD内任一点，若AB=3，BC=4.则图中阴影部分的面积为 ．
13. 如图，矩形ABCD中，AB=2 ，AD=6，P为边AD上一点，且AP=2，在对角线BD上寻找一点M，使AM+PM最小，则AM+PM的最小值为 ．
14. 如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB＝6 cm，BC＝8 cm，则△AEF的周长为cm．
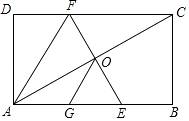
15. 在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，则EF的最小值为 ．
16. 如图，在矩形ABCD中，O为AC中点，EF过点O且EF⊥AC分别交DC于点F，交AB于点E，点G是AE中点且∠AOG=30°，给出以下结论：①∠AFC=120°；
②△AEF是等边三角形；
③AC=3OG；
④S△AOG= S△ABC
其中正确的是 ． （把所有正确结论的序号都选上）
三、解答题
-
17. 如图，菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，且DE∥AC，AE∥BD．求OE的长．
18. 如图，在矩形ABCD中，点E在边AD上，EF⊥CE且与AB相交于点F，若DE=2，AD+DC=8，且CE=EF，求AE的长。
19. 如图，在矩形ABCD中，M，N分别是AD，BC的中点，E，F分别是线段BM，CM的中点，若AB=8，AD=12，则四边形ENFM的周长是多少？
20. 如图，已知▱ABCD，延长AB到E使BE=AB，连接BD，ED，EC，若ED=AD．
(1)、求证：四边形BECD是矩形；(2)、连接AC，若AD=4，CD= 2，求AC的长．
