2018-2019学年数学北师大版九年级上册1.2 矩形的性质与判定（2） 同步训练
试卷更新日期：2018-08-17 类型：同步测试
一、选择题
-
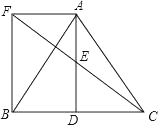
1. 如图， 的对角线 与 相交于点 ，要使它成为矩形，需再添加的条件是（ ）
A、 B、 C、 D、 平分2. 如图所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，若AB=3，BC=4，那么阴影部分的面积为（ ）
A、4 B、12 C、6 D、33. 有一根长60cm的铁丝，用它围成一个矩形，写出矩形面积S（ ）与它的一边长 之间的函数关系式为（ ）A、 B、 C、 D、4. 如图，矩形ABCD沿着AE折叠，使D点落在BC边上的F点处，如果 等于（ ）
A、 B、 C、 D、5. 如图，E，F，G，H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（ ）
A、对角线互相垂直 B、对角线相等 C、一组对边平行而另一组对边不平行 D、对角线互相平分6. 下列识别图形不正确的是（ ）A、有一个角是直角的平行四边形是矩形 B、有三个角是直角的四边形是矩形 C、对角线相等的四边形是矩形 D、对角线互相平分且相等的四边形是矩形7. 已知：线段AB，BC，∠ABC=90°．求作：矩形ABCD．以下是甲、乙两同学的作业：
对于两人的作业，下列说法正确的是（ ）
A、两人都对 B、两人都不对 C、甲对，乙不对 D、甲不对，乙对8. 顺次连接菱形各边中点所形成的四边形是（ ）
A、平行四边形 B、菱形 C、 矩形 D、正方形9. 在△ABC中，点D是边BC上的点（与B，C两点不重合），过点D作DE∥AC，DF∥AB，分别交AB，AC于E，F两点，下列说法正确的是（ ）
A、若AD⊥BC，则四边形AEDF是矩形 B、若AD垂直平分BC，则四边形AEDF是矩形 C、若BD=CD，则四边形AEDF是菱形 D、若AD平分∠BAC，则四边形AEDF是菱形10.已知：如图，在▱ABCD中，点E在AD上，连接BE，DF∥BE交BC于点F，AF与BE交于点M，CE与DF交于点N，AF，BE分别平分∠BAD，∠ABC；CE，DF分别平分∠BCD，∠ADC，则四边形MFNE是（ ）
A、菱形 B、矩形 C、平行四边形 D、正方形二、填空题
-
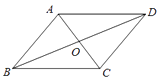
11. 要使平行四边形ABCD是矩形，还需添加的条件是(写出一种即可).12. 如图，在四边形ABCD中，AC，BD相交于点O，AO＝OC，BO＝OD，∠ABC＝90°，则四边形ABCD是；若AC＝5 cm，则BD＝ ．
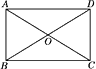13. 四边形ABCD中，AC⊥BD，顺次连接它的各边中点所得的四边形是.14. 如图，平行四边形的四个内角平分线相交，如能构成四边形，则这个四边形是
15. 如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE，已知菱形ABCD的周长为20 cm，则 OE长为cm．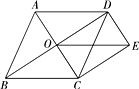
16. 如图，矩形ABCD中，AB=8cm，BC=3cm，E是DC的中点，BF= FC，则四边形DBFE的面积为cm2 ．
三、解答题
-
17. 如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．
18. 如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F，连接AC、BE．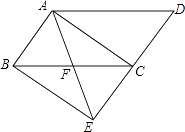
(1)、你判断四边形ABEC形状是 ；(2)、请你添加一个条件，使四边形ABEC是矩形，并请说明理由；
(3)、当△ABC满足 条件时，四边形ABEC是菱形．（不需说理）
19. 如图，在▱ABCD中，点E是边CD的中点，连接BE并延长，交AD延长线于点F，连接BD、CF.
(1)、求证：△CEB≌△DEF；(2)、若AB=BF，试判断四边形BCFD的形状，并证明．
20. 如图，在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形，AC、DE相交于点O．
(1)、求证：四边形ADCE是矩形．(2)、若∠AOE=60°，AE=4，求矩形ADCE对角线的长．
21. 如图，DB∥AC，且DB=AC，E是AC的中点．
(1)、求证：BC=DE；(2)、连接AD、BE，若∠BAC=∠C，求证：四边形DBEA是矩形．
