2018-2019学年数学北师大版九年级上册1.1 菱形的性质与判定（2） 同步训练

试卷更新日期：2018-08-17 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 如图，在▱ABCD中，对角线 AC ， BD 相交于点O，添加下列条件不能判定▱ABCD是菱形的只有（   ）

    A、AC⊥BD B、AB=BC C、AC=BD D、∠1=∠2

    查看试题解析

  • 2. 下列命题中正确的是（   ）
    A、对角线相等的四边形是菱形 B、对角线互相垂直的四边形是菱形 C、对角线相等的平行四边形是菱形 D、对角线互相垂直的平行四边形是菱形

    查看试题解析

  • 3. 已知四边形ABCD是平行四边形，如果要使它成为菱形，那么需要添加的条件是（     ）
    A、AB=CD ； B、AB=BC  ； C、AD=BC ； D、AC=BD ．

    查看试题解析

  • 4. 四边形的四边长顺次为a、b、c、d，且a2+b2+c2+d2=ab+bc+cd+ad，则此四边形一定是（   ）
    A、平行四边形 B、矩形 C、菱形 D、正方形

    查看试题解析

  • 5. 在平面直角坐标系中，已知点A（0，2），B（﹣2 3 ，0），C（0，﹣2），D（2 3 ，0），则以这四个点为顶点的四边形ABCD是（   ）
    A、矩形 B、菱形 C、正方形 D、梯形

    查看试题解析

  • 6. 红丝带是关注艾滋病防治问题的国际性标志，人们将红丝带剪成小段，并用别针将折叠好的红丝带别在胸前，如图所示．红丝带重叠部分形成的图形是（   ）

    A、正方形 B、等腰梯形 C、菱形 D、矩形

    查看试题解析

  • 7. 如图，在平面直角坐标系xOy中，已知点A（ 2 ，0），B（1，1）．若平移点A到点C，使以点O，A，C，B为顶点的四边形是菱形，则正确的平移方法是（   ）

    A、向左平移1个单位，再向下平移1个单位 B、向左平移（ 22−1 ）个单位，再向上平移1个单位 C、向右平移 2 个单位，再向上平移1个单位 D、向右平移1个单位，再向上平移1个单位

    查看试题解析

  • 8.

    如图，是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：对于甲、乙两人的作法，可判断（　　）

    A、甲正确，乙错误  B、甲错误，乙正确 C、甲、乙均正确 D、甲、乙均错误

    查看试题解析

  • 9. 如图，以A点为圆心，以相同的长为半径作弧，分别与射线AM，AN交于B，C两点，连接BC，再分别以B，C为圆心，以相同长（大于 12 BC）为半径作弧，两弧相交于点D，连接AD，BD，CD．则下列结论错误的是（   ）

    A、AD平分∠MAN B、AD垂直平分BC C、∠MBD=∠NCD D、四边形ACDB一定是菱形

    查看试题解析

二、填空题

  • 10. 在四边形ABCD中，对角线AC、BD交于点O，从（1）AB=CD；（2）AB∥CD；（3）OA=OC；（4）OB=OD；（5）AC⊥BD；（6）AC平分∠BAD这六个条件中，选取三个推出四边形ABCD是菱形．如（1）（2）（5）⇒ABCD是菱形，再写出符合要求的两个：⇒ABCD是菱形；⇒ABCD是菱形．

    查看试题解析

  • 11. 如图所示，将两张等宽的长方形条交叉叠放，重叠部分是一个四边形ABCD，若AD=4cm，∠ABC=30°，则四边形ABCD的面积是cm2 ．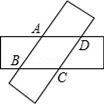

    查看试题解析

  • 12. 如图，在 ▱ ABCD中，对角线AC，BD相交于点O，若再增加一个条件，就可得出 ▱ ABCD是菱形，则你添加的条件是 ．

    查看试题解析

  • 13. 如图，DE∥AC交AB于点E，DF∥AB交AC于F，∠1=∠2，四边形AEDF的形状是 ．

    查看试题解析

  • 14. 在数学课上，老师提出如下问题：

    如图1，将锐角三角形纸片ABC（BC＞AC）经过两次折叠，得到边AB，BC，CA上的点D，E，F．使得四边形DECF恰好为菱形．小明的折叠方法如下：

    如图2，（1）AC边向BC边折叠，使AC边落在BC边上，得到折痕交AB于D；（2）C点向AB边折叠，使C点与D点重合，得到折痕交BC边于E，交AC边于F．
    老师说：“小明的作法正确．”
    请回答：小明这样折叠的依据是 ．

    查看试题解析

  • 15. 如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形 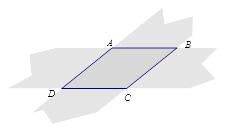ABCD 中， AB=3 ， AC=2 ，则 BD 的长为 ．

    查看试题解析

三、解答题

  • 16. 如图，△ABC≌△ABD，点E在边AB上，并且CE∥BD，连接DE.

    求证：四边形BCED是菱形.

    查看试题解析

  • 17. 如图，将平行四边形ABCD沿过点A的直线l折叠，使点D落到AB边上的点F处，折痕交CD边于点E.

    求证：四边形ADEF是菱形.

    查看试题解析

  • 18. 如图，在▱ABCD中，O为AC的中点，过点O作EF⊥AC与边AD、BC分别相交于点E、F，求证：四边形AECF是菱形．

    查看试题解析

  • 19. 如图，在四边形ABCD中，AD∥BC，AM⊥BC，垂足为M，AN⊥DC，垂足为N，若∠BAD=∠BCD，AM=AN．

    求证：四边形ABCD是菱形．

    查看试题解析

  • 20. 如图：在△ABC中，∠BAC = 90° ，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F，求证：四边形AEFG是菱形.

    查看试题解析

  • 21. 如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD的中点．

    (1)、求证：四边形PMEN是平行四边形；
    (2)、当AP为何值时，四边形PMEN是菱形？并给出证明。

    查看试题解析