辽宁省抚顺市2018年中考数学试卷

试卷更新日期：2018-08-17 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣ $\frac{3}{2}$ 的绝对值是（）

A、﹣ $\frac{2}{3}$ B、 $\frac{2}{3}$ C、﹣ $\frac{3}{2}$ D、 $\frac{3}{2}$

查看试题解析
2. 下列物体的左视图是圆的是（）

A、足球 B、水杯 C、圣诞帽 D、鱼缸

查看试题解析
3. 下列运算正确的是（）

A、2x+3y=5xy B、（x+3）²=x²+9 C、（xy²）³=x³y⁶ D、x¹⁰÷x⁵=x²

查看试题解析
4. 二次根式 $\sqrt{1 - x}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥1 B、x≤1 C、x＞1 D、x＜1

查看试题解析
5. 抚顺市中小学机器人科技大赛中，有7名学生参加决赛，他们决赛的成绩各不相同，其中一名参赛选手想知道自己能否进入前4名，他除了知道自己成绩外还要知道这7名学生成绩的（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
6. 一次函数y=﹣x﹣2的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第一、三，四象限 D、第二、三、四象限

查看试题解析
7. 已知点A的坐标为（1，3），点B的坐标为（2，1）．将线段AB沿某一方向平移后，点A的对应点的坐标为（﹣2，1）．则点B的对应点的坐标为（）

A、（5，3） B、（﹣1，﹣2） C、（﹣1，﹣1） D、（0，﹣1）

查看试题解析
8. 如图，AB是⊙O的直径，CD是弦，∠BCD=30°，OA=2，则阴影部分的面积是（）

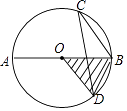A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、π D、2π

查看试题解析
9. 如图，菱形ABCD的边AD与x轴平行，A，B两点的横坐标分别为1和3，反比例函数y= $\frac{3}{x}$ 的图象经过A，B两点，则菱形ABCD的面积是（）

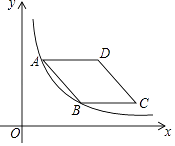A、4 $\sqrt{2}$ B、4 C、2 $\sqrt{2}$ D、2

查看试题解析
10. 已知抛物线y=ax²+bx+c（0＜2a≤b）与x轴最多有一个交点．以下四个结论：
①abc＞0；②该抛物线的对称轴在x=﹣1的右侧；③关于x的方程ax²+bx+c+1=0无实数根；④ $\frac{a + b + c}{b}$ ≥2．其中，正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 第十三届全国人民代表大会政府工作报告中说到，五年来我国国内生产总值已增加到8270000000万元，将数据8270000000用科学记数法表示为．

查看试题解析
12. 分解因式：xy²﹣4x= ．

查看试题解析
13. 甲，乙两名跳高运动员近期20次的跳高成绩统计分析如下： $\bar{x_{甲}}$ =1.70m， $\bar{x_{乙}}$ =1.70m，s_甲²=0.007，s_乙²=0.003，则两名运动员中，的成绩更稳定．

查看试题解析
14. 一个不透明布袋里有3个红球，4个白球和m个黄球，这些球除颜色外其余都相同，若从中随机摸出1个球是红球的概率为 $\frac{1}{3}$ ，则m的值为．

查看试题解析
15. 将两张三角形纸片如图摆放，量得∠1+∠2+∠3+∠4=220°，则∠5=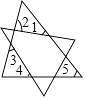

查看试题解析
16. 如图，▱ABCD中，AB=7，BC=3，连接AC，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径作弧，两弧相交于点M，N，作直线MN，交CD于点E，连接AE，则△AED的周长是．

查看试题解析
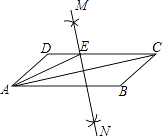17. 如图，△AOB三个顶点的坐标分别为A（8，0），O（0，0），B（8，﹣6），点M为OB的中点．以点O为位似中心，把△AOB缩小为原来的 $\frac{1}{2}$ ，得到△A′O′B′，点M′为O′B′的中点，则MM′的长为．

查看试题解析
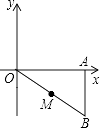18. 如图，正方形AOBO₂的顶点A的坐标为A（0，2），O₁为正方形AOBO₂的中心；以正方形AOBO₂的对角线AB为边，在AB的右侧作正方形ABO₃A₁ ， O₂为正方形ABO₃A₁的中心；再以正方形ABO₃A₁的对角线A₁B为边，在A₁B的右侧作正方形A₁BB₁O₄ ， O₃为正方形A₁BB₁O₄的中心；再以正方形A₁BB₁O₄的对角线A₁B₁为边在A₁B₁的右侧作正方形A₁B₁O₅A₂ ， O₄为正方形A₁B₁O₅A₂的中心：…；按照此规律继续下去，则点O₂₀₁₈的坐标为．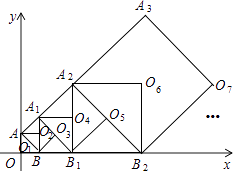

查看试题解析

三、解答题

19. 先化简，再求值：（1﹣x+ $\frac{3}{x + 1}$ ）÷ $\frac{x^{2} + 4 x + 4}{x + 1}$ ，其中x=tan45°+（ $\frac{1}{2}$ ）^﹣1 ．

查看试题解析
20. 抚顺市某校想知道学生对“遥远的赫图阿拉”，“旗袍故里”等家乡旅游品牌的了解程度，随机抽取了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必选且只选一项）A．十分了解，B．了解较多，C．了解较少，D．不知道．将调查的结果绘制成如下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：

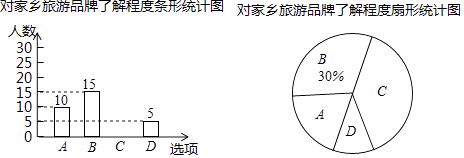(1)、本次调查了多少名学生？

(2)、补全条形统计图；

(3)、该校共有500名学生，请你估计“十分了解”的学生有多少名？

(4)、在被调查“十分了解”的学生中有四名学生会干部，他们中有3名男生和1名女生，学校想从这4人中任选两人做家乡旅游品牌宣传员，请用列表或画树状图法求出被选中的两人恰好是一男一女的概率．

查看试题解析

四、解答题

21. 如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．

(1)、求灯杆CD的高度；

(2)、求AB的长度（结果精确到0.1米）．（参考数据： $\sqrt{3}$ =1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）

查看试题解析
22. 为落实“美丽抚顺”的工作部署，市政府计划对城区道路进行了改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的 $\frac{3}{2}$ 倍，甲队改造360米的道路比乙队改造同样长的道路少用3天．

(1)、甲、乙两工程队每天能改造道路的长度分别是多少米？

(2)、若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1200米，改造总费用不超过145万元，至少安排甲队工作多少天？

查看试题解析

五、解答验

23. 如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB、连接DO并延长交CB的延长线于点E．

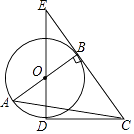(1)、判断直线CD与⊙O的位置关系，并说明理由；

(2)、若BE=4，DE=8，求AC的长．

查看试题解析

六、解答题

24. 俄罗斯世界杯足球赛期间，某商店销售一批足球纪念册，每本进价40元，规定销售单价不低于44元，且获利不高于30%．试销售期间发现，当销售单价定为44元时，每天可售出300本，销售单价每上涨1元，每天销售量减少10本，现商店决定提价销售．设每天销售量为y本，销售单价为x元．

(1)、请直接写出y与x之间的函数关系式和自变量x的取值范围；

(2)、当每本足球纪念册销售单价是多少元时，商店每天获利2400元？

(3)、将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润w元最大？最大利润是多少元？

查看试题解析

七、解答题

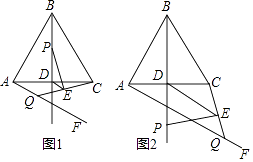
25. 如图，△ABC中，AB=BC，BD⊥AC于点D，∠FAC= $\frac{1}{2}$ ∠ABC，且∠FAC在AC下方．点P，Q分别是射线BD，射线AF上的动点，且点P不与点B重合，点Q不与点A重合，连接CQ，过点P作PE⊥CQ于点E，连接DE．

(1)、若∠ABC=60°，BP=AQ．
①如图1，当点P在线段BD上运动时，请直接写出线段DE和线段AQ的数量关系和位置关系；
②如图2，当点P运动到线段BD的延长线上时，试判断①中的结论是否成立，并说明理由；

(2)、若∠ABC=2α≠60°，请直接写出当线段BP和线段AQ满足什么数量关系时，能使（1）中①的结论仍然成立（用含α的三角函数表示）．

查看试题解析

八、解答题

26. 如图，抛物线y=﹣x²+bx+c和直线y=x+1交于A，B两点，点A在x轴上，点B在直线x=3上，直线x=3与x轴交于点C

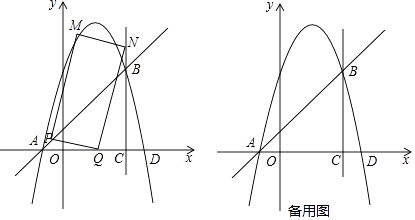(1)、求抛物线的解析式；

(2)、点P从点A出发，以每秒 $\sqrt{2}$ 个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒（t＞0）．以PQ为边作矩形PQNM，使点N在直线x=3上．
①当t为何值时，矩形PQNM的面积最小？并求出最小面积；
②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上．

查看试题解析