湖北省十堰市2018年中考数学试卷

试卷更新日期：2018-08-17 类型：中考真卷

进入出卷网下载

一、选择题

1. 在0，﹣1，0.5，（﹣1）²四个数中，最小的数是（）

A、0 B、﹣1 C、0.5 D、（﹣1）²

查看试题解析
2. 如图，直线a∥b，将一直角三角形的直角顶点置于直线b上，若∠1=28°，则∠2的度数是（）

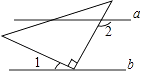A、62° B、108° C、118° D、152°

查看试题解析
3. 今年“父亲节”佳佳给父亲送了一个礼盒，该礼盒的主视图是（）

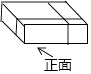A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、2x+3y=5xy B、（﹣2x²）³=﹣6x⁶ C、3y²•（﹣y）=﹣3y² D、6y²÷2y=3y

查看试题解析
5. 某体育用品商店一天中卖出某种品牌的运动鞋15双，其中各种尺码的鞋的销售量如表所示：
鞋的尺码/cm
23
23.5
24
24.5
25
销售量/双
1
3
3
6
2
则这15双鞋的尺码组成的一组数据中，众数和中位数分别为（）

A、24.5，24.5 B、24.5，24 C、24，24 D、23.5，24

查看试题解析
6. 菱形不具备的性质是（）

A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形

查看试题解析
7. 我国古代数学著作《九章算术》卷七有下列问题：“今有共买物，人出八，盈三：人出七，不足四，问人数、物价几何？”意思是：现在有几个人共同出钱去买件物品，如果每人出8钱，则剩余3钱：如果每人出7钱，则差4钱．问有多少人，物品的价格是多少？设有x人，物品的价格为y元，可列方程（组）为（）

A、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 $\frac{x + 3}{8} = \frac{x - 4}{7}$ D、 $\frac{y - 3}{8}$ = $\frac{y + 4}{7}$

查看试题解析
8. 如图，是按一定规律排成的三角形数阵，按图中数阵的排列规律，第9行从左至右第5个数是（）

A、2 $\sqrt{10}$ B、 $\sqrt{41}$ C、5 $\sqrt{2}$ D、 $\sqrt{51}$

查看试题解析
9. 如图，扇形OAB中，∠AOB=100°，OA=12，C是OB的中点，CD⊥OB交 $\overset{⌢}{A B}$ 于点D，以OC为半径的 $\overset{⌢}{C E}$ 交OA于点E，则图中阴影部分的面积是（）

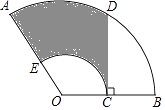A、12π+18 $\sqrt{3}$ B、12π+36 $\sqrt{3}$ C、6 $π + 18 \sqrt{3}$ D、6 $π + 36 \sqrt{3}$

查看试题解析
10. 如图，直线y=﹣x与反比例函数y= $\frac{k}{x}$ 的图象交于A，B两点，过点B作BD∥x轴，交y轴于点D，直线AD交反比例函数y= $\frac{k}{x}$ 的图象于另一点C，则 $\frac{C B}{C A}$ 的值为（）

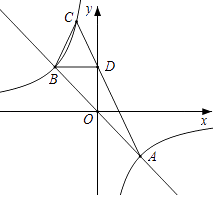A、1：3 B、1：2 $\sqrt{2}$ C、2：7 D、3：10

查看试题解析

二、填空题

11. 北京时间6月5日21时07分，中国成功将风云二号H气象卫星送入预定的高度36000km的地球同步轨道，将36000km用科学记数法表示为．

查看试题解析
12. 函数 $y = \sqrt{x - 3}$ 的自变量x的取值范围是．

查看试题解析
13. 如图，已知▱ABCD的对角线AC，BD交于点O，且AC=8，BD=10，AB=5，则△OCD的周长为．

查看试题解析
14. 对于实数a，b，定义运算“※”如下：a※b=a²﹣ab，例如，5※3=5²﹣5×3=10．若（x+1）※（x﹣2）=6，则x的值为．

查看试题解析
15. 如图，直线y=kx+b交x轴于点A，交y轴于点B，则不等式x（kx+b）＜0的解集为．

查看试题解析
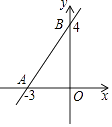16. 如图，Rt△ABC中，∠BAC=90°，AB=3，AC=6 $\sqrt{2}$ ，点D，E分别是边BC，AC上的动点，则DA+DE的最小值为．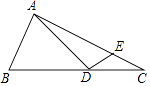

查看试题解析

三、解答题

17. 计算：|﹣ $\sqrt{3}$ |﹣2^﹣1+ $\sqrt{12}$

查看试题解析
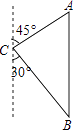
18. 化简： $\frac{1}{a - 1}$ ﹣ $\frac{1}{a^{2} + a}$ ÷ $\frac{a^{2} - 1}{a^{2} + 2 a + 1}$

查看试题解析
19. 如图，一艘海轮位于灯塔C的北偏东45方向，距离灯塔100海里的A处，它沿正南方向航行一段时间后，到达位于灯塔C的南偏东30°方向上的B处，求此时船距灯塔的距离（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732，结果取整数）．

查看试题解析
20. 今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级
成绩（s）
频数（人数）
A
90＜s≤100
4
B
80＜s≤90
x
C
70＜s≤80
16
D
s≤70
6
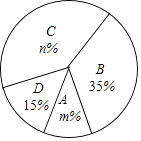
根据以上信息，解答以下问题：

(1)、表中的x=；

(2)、扇形统计图中m= ， n= ， C等级对应的扇形的圆心角为度；

(3)、该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a₁ ， a₂表示）和两名女生（用b₁ ， b₂表示），请用列表或画树状图的方法求恰好选取的是a₁和b₁的概率．

查看试题解析
21. 已知关于x的一元二次方程x²﹣（2k﹣1）x+k²+k﹣1=0有实数根．

(1)、求k的取值范围；

(2)、若此方程的两实数根x₁ ， x₂满足x₁²+x₂²=11，求k的值．

查看试题解析
22. 为早日实现脱贫奔小康的宏伟目标，我市结合本地丰富的山水资源，大力发展旅游业，王家庄在当地政府的支持下，办起了民宿合作社，专门接待游客，合作社共有80间客房．根据合作社提供的房间单价x（元）和游客居住房间数y（间）的信息，乐乐绘制出y与x的函数图象如图所示：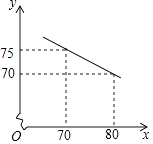

(1)、求y与x之间的函数关系式；

(2)、合作社规定每个房间价格不低于60元且不超过150元，对于游客所居住的每个房间，合作社每天需支出20元的各种费用，房价定为多少时，合作社每天获利最大？最大利润是多少？

查看试题解析
23. 如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作FG⊥AC于点F，交AB的延长线于点G．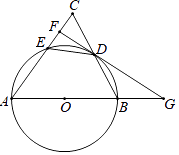

(1)、求证：FG是⊙O的切线；

(2)、若tanC=2，求 $\frac{G B}{G A}$ 的值．

查看试题解析
24. 已知正方形ABCD与正方形CEFG，M是AF的中点，连接DM，EM．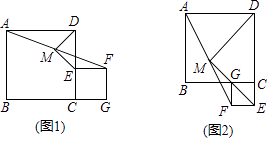

(1)、如图1，点E在CD上，点G在BC的延长线上，请判断DM，EM的数量关系与位置关系，并直接写出结论；

(2)、如图2，点E在DC的延长线上，点G在BC上，（1）中结论是否仍然成立？请证明你的结论；

(3)、将图1中的正方形CEFG绕点C旋转，使D，E，F三点在一条直线上，若AB=13，CE=5，请画出图形，并直接写出MF的长．

查看试题解析
25. 已知抛物线y= $\frac{1}{2}$ x²+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．

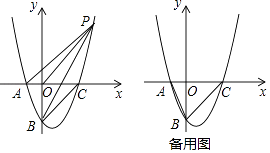(1)、求抛物线的解析式；

(2)、如图，P是第一象限内抛物线上一点，且S_△PBO=S_△PBC ，求证：AP∥BC；

(3)、在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．

查看试题解析

等级	成绩（s）	频数（人数）
A	90＜s≤100	4
B	80＜s≤90	x
C	70＜s≤80	16
D	s≤70	6

鞋的尺码/cm	23	23.5	24	24.5	25
销售量/双	1	3	3	6	2