2015-2016学年浙江省杭州市锦绣育才教育集团八年级下学期期中数学试卷

试卷更新日期：2017-02-22 类型：期中考试

进入出卷网下载

一、仔细选一选

1. 以下四个汽车标志中，是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、2 $\sqrt{3}$ ﹣ $\sqrt{3}$ =1 B、（﹣ $\sqrt{2}$ ）²=2 C、 $\sqrt{3^{2} - 2^{2}}$ = $\sqrt{3^{2}}$ ﹣ $\sqrt{2^{2}}$ =3﹣2=1 D、 $\sqrt{{(- 11)}^{2}}$ =±11

查看试题解析
3. 如图是某学校全体教职工年龄的频数分布直方图（每组年龄包含最小值，不包含最大值），根据图形提供的信息，下列说法中错误的是（）

A、该学校教职工总人数是50人 B、这一组年龄在40≤x＜42小组的教职工人数占该学校全体教职工总人数的20% C、教职工年龄的中位数一定落在40≤x＜42这一组 D、教职工年龄的众数一定在38≤x＜40这一组

查看试题解析
4. 如果式子 $\sqrt{{(x - 3)}^{2}} - | x - 2 |$ 化简的结果为5﹣2x，则x的取值范围是（）

A、x≥3 B、x≤2 C、x≥2 D、2≤x≤3

查看试题解析
5. 如图，在▱ABCD中，∠A=70°，将▱ABCD折叠，使点D，C分别落在点F，E处（点F，E都在AB所在的直线上），折痕为MN，则∠AMF等于（）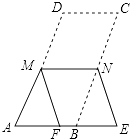

A、70° B、40° C、30° D、20°

查看试题解析
6. 已知四边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么可以判定四边形ABCD是平行四边形的是（）
①再加上条件“BC=AD”，则四边形ABCD一定是平行四边形．
②再加上条件“∠BAD=∠BCD”，则四边形ABCD一定是平行四边形．
③再加上条件“AO=CO”，则四边形ABCD一定是平行四边形．
④再加上条件“∠DBA=∠CAB”，则四边形ABCD一定是平行四边形．

A、①和② B、①③和④ C、②和③ D、②③和④

查看试题解析
7. 为执行“均衡教育”政策，某县2014年投入教育经费2500万元，预计到2016年底三年累计投入1.2亿元．若每年投入教育经费的年平均增长百分率为x，则下列方程正确的是（　　）

A、2500（1+x）²=1.2 B、2500（1+x）²=12000 C、2500+2500（1+x）+2500（1+x）²=1.2 D、2500+2500（1+x）+2500（1+x）²=12000

查看试题解析
8. 用反证法证明命题“四边形中至少有一个角是钝角或直角”，应先假设（　　）

A、四边形中没有一个角是钝角或直角 B、四边形中至多有一个钝角或直角 C、四边形中没有一个角是锐角 D、四边形中没有一个角是钝角

查看试题解析
9. 如图，△ABC中，AB=4，AC=3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为（）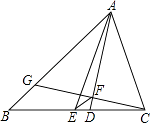

A、 $\frac{1}{2}$ B、1 C、 $\frac{7}{2}$ D、7

查看试题解析
10. 对于实数a、b，定义一种运算“⊗”为：a⊗b=a²+ab﹣2，有下列命题：
①1⊗3=2；②方程x⊗1=0的根为：x₁=﹣2，x₂=1；
③不等式组 ${\begin{matrix} (- 2) \otimes x - 4 < 0 \\ 1 \otimes x - 3 < 0 \end{matrix}$ 的解集为：﹣1＜x＜4；
其中正确的是（）

A、①②③ B、①③ C、①② D、②③

查看试题解析

二、认真填一填

11. 化简计算： $\sqrt{{(- 2)}^{2}}$ = ， $\frac{2}{\sqrt{3} + 1}$ = ．

查看试题解析
12. 一个多边形的每一个内角都是140°，则这个多边形是边形．

查看试题解析
13. 若 $\frac{\sqrt{x + 4}}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
14. 已知一组数据：x₁ ， x₂ ， x₃ ， …x_n的平均数是2，方差是3，另一组数据：3x₁﹣2，3x₂﹣2，…3x_n﹣2的方差是．

查看试题解析
15. 由10块相同的小长方形地砖拼成面积为1.6m²的长方形ABCD（如图），则长方形ABCD的周长为．

查看试题解析
16. 在平行四边形ABCD中，BC边上的高为4，AB=5，AC=2 $\sqrt{5}$ ，则平行四边形ABCD的周长等于．

查看试题解析

三、全面答一答

17. 某学校抽查了某班级某月5天的用电量，数据如下表（单位：度）：
度数
9
10
11
天数
3
1
1

(1)、求这5天的用电量的平均数；

(2)、求这5天用电量的众数、中位数；

(3)、学校共有36个班级，若该月按22天计，试估计该校该月的总用电量．

查看试题解析
18. 计算与解方程

(1)、计算： $\sqrt{18}$ ﹣（ $\sqrt{2}$ +1）^﹣¹+（ $\sqrt{3}$ ﹣ $\sqrt{2}$ ）⁰

(2)、用适当的方法解下列方程：
①x²﹣12x﹣4=0；
②（x﹣1）²+2x（x﹣1）=0．

查看试题解析
19. 按要求解决下列问题：

(1)、化简下列各式：
$\frac{2}{\sqrt{1}}$ = ， $\frac{8}{\sqrt{2}}$ = ， $\frac{18}{\sqrt{3}}$ = ， $\frac{50}{\sqrt{5}}$ = ， …

(2)、通过观察，归纳写出能反映这个规律的一般结论，并证明．

查看试题解析
20. 某租赁公司拥有汽车100辆．据统计，每辆车的月租金为4000元时，可全部租出．每辆车的月租金每增加100元，未租出的车将增加1辆．租出的车每辆每月的维护费为500元，未租出的车每辆每月只需维护费100元．

(1)、当每辆车的月租金为4600元时，能租出多少辆？并计算此时租赁公司的月收益（租金收入扣除维护费）是多少万元？

(2)、规定每辆车月租金不能超过7200元，当每辆车的月租金定为多少元时，租赁公司的月收益（租金收入扣除维护费）可达到40.4万元？

查看试题解析
21. 如图，在▱ABCD中，∠DAB=60°，点E，F分别在CD，AB的延长线上，且AE=AD，CF=CB．

(1)、求证：四边形AFCE是平行四边形；

(2)、若去掉已知条件“∠DAB=∠60°”，（1）中的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．

查看试题解析
22. 如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合），连接AD，作BE⊥AD，垂足为E，连接CE，过点E作EF⊥CE，交BD于F．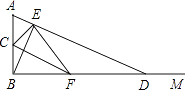

(1)、求证：BF=FD；

(2)、点D在运动过程中能否使得四边形ACFE为平行四边形？如不能，请说明理由；如能，求出此时∠A的度数．

查看试题解析
23. 如果方程x²+px+q=0的两个根是x₁ ， x₂ ，那么x₁+x₂=﹣p，x₁•x₂=q，请根据以上结论，解决下列问题：

(1)、若p=﹣4，q=3，求方程x²+px+q=0的两根．

(2)、已知实数a、b满足a²﹣15a﹣5=0，b²﹣15b﹣5=0，求 $\frac{a}{b}$ + $\frac{b}{a}$ 的值；

(3)、已知关于x的方程x²+mx+n=0，（n≠0），求出一个一元二次方程，使它的两个根分别是已知方程两根的倒数．

查看试题解析

度数	9	10	11
天数	3	1	1