2015-2016学年浙江省杭州市大江东区八年级下学期期中数学试卷

试卷更新日期：2017-02-22 类型：期中考试

进入出卷网下载

一、仔细选一选

1. 要使式子 $\sqrt{2 - x}$ 有意义，则x的取值范围是（）

A、x＞0 B、x≥﹣2 C、x≥2 D、x≤2

查看试题解析
2. 下列运算正确的是（）

A、2 $\sqrt{3}$ ﹣ $\sqrt{3}$ =1 B、（﹣ $\sqrt{2}$ ）²=2 C、 $\sqrt{{(- 11)}^{2}}$ =±11 D、 $\sqrt{3^{2} - 2^{2}}$ = $\sqrt{3^{2}} - \sqrt{2^{2}}$ =3﹣2=1

查看试题解析
3. 在某校“我的中国梦”演讲比赛中，有9名学生参加比赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（　　）

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
4. 用配方法解方程x²+8x+7=0，则配方正确的是（）

A、（x+4）²=9 B、（x﹣4）²=9 C、（x﹣8）²=16 D、（x+8）²=57

查看试题解析
5. 如果关于x的一元二次方程x²+px+q=0的两根分别为x₁=3，x₂=1，那么这个一元二次方程是（）

A、x²+3x+4=0 B、x²+4x﹣3=0 C、x²﹣4x+3=0 D、x²+3x﹣4=0

查看试题解析
6. 如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件 $\underset{\cdot}{不} \underset{\cdot}{能}$ 是（）

A、AE=CF B、BE=FD C、BF=DE D、∠1=∠2

查看试题解析
7. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如表所示：
用电量（度）
120
140
160
180
200
户数
2
3
6
7
2
则这20户家庭该月用电量的众数和中位数分别是（）

A、180，160 B、160，180 C、160，160 D、180，180

查看试题解析
8. 在▱ABCD中，∠ACB=25°，现将▱ABCD沿EF折叠，使点C与点A重合，点D落在G处，则∠GFE的度数（）

A、135° B、120° C、115° D、100°

查看试题解析
9. 关于x的方程x²+2kx+k﹣1=0的根的情况描述正确的是（）

A、k为任何实数，方程都没有实数根 B、k为任何实数，方程都有两个不相等的实数根 C、k为任何实数，方程都有两个相等的实数根 D、根据k的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种

查看试题解析
10. 如图，已知△ABC中，∠ABC=90°，AB=BC，三角形的顶点在相互平行的三条直线l₁ ， l₂ ， l₃上，且l₁ ， l₂之间的距离为2，l₂ ， l₃之间的距离为3，则AC的长是（）

A、 $2 \sqrt{17}$ B、 $2 \sqrt{5}$ C、 $4 \sqrt{2}$ D、7

查看试题解析

二、认真填一填

11. 已知一个无理数与 $\sqrt{2}$ +1的积为有理数，这个无理数为．

查看试题解析
12. 一元二次方程（a﹣1）x²+x+a²﹣1=0一根为0，则a= ．

查看试题解析
13. 一个多边形截去一个角后其内角和为9000°，那么这个多边形的边数为．

查看试题解析
14. 若（x²+y²）（x²+y²﹣1）=12，则x²+y²= .

查看试题解析
15. 已知a=4，b，c是方程x²﹣5x+6=0的两个根，则以a、b、c为三边的三角形面积是．

查看试题解析
16. 如图，在▱ABCD中，点E在BC上，AE平分∠BAD，且AB=AE，连接DE并延长与AB的延长线交于点F，连接CF，若AB=1cm，则△CEF面积是 cm² ．

查看试题解析

三、全面答一答

17. 计算

(1)、 $\sqrt{8}$ + $\sqrt{32}$ ﹣ $\sqrt{2}$

(2)、（3+ $\sqrt{2}$ ）（3﹣ $\sqrt{2}$ ）+（1+ $\sqrt{2}$ ）² ．

查看试题解析
18. 解方程：

(1)、3x²﹣7x=0

(2)、（x﹣2）（2x﹣3）=2（x﹣2）

查看试题解析
19. 八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如表（10分制）：
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9

(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算甲、乙队的平均成绩和方差，试说明成绩较为整齐的是哪一队？

查看试题解析
20. 如图，在▱ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．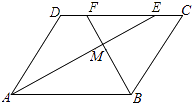

(1)、试说明：AE⊥BF；

(2)、判断线段DF与CE的大小关系，并予以说明．

查看试题解析
21. 水库大坝截面的迎水坡坡比（DE与AE的长度之比）为1：0.6，背水坡坡比为1：2，大坝高DE=30米，坝顶宽CD=10米，求大坝的截面的周长和面积．

查看试题解析
22. 现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．

(1)、求该快递公司投递总件数的月平均增长率；

(2)、如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？

查看试题解析
23. 如图，在边长为12cm的等边三角形ABC中，点P从点A开始沿AB边向点B以每秒钟1cm的速度移动，点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动．若P、Q分别从A、B同时出发，其中任意一点到达目的地后，两点同时停止运动，求：

(1)、经过6秒后，BP=cm，BQ=cm；

(2)、经过几秒后，△BPQ是直角三角形？

(3)、经过几秒△BPQ的面积等于 $10 \sqrt{3}$ cm²？

查看试题解析

用电量（度）	120	140	160	180	200
户数	2	3	6	7	2

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9