2017年上海市宝山区中考数学一模试卷

试卷更新日期：2017-02-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 已知∠A=30°，下列判断正确的是（）

A、sinA= $\frac{1}{2}$ B、cosA= $\frac{1}{2}$ C、tanA= $\frac{1}{2}$ D、cotA= $\frac{1}{2}$

查看试题解析
2. 如果C是线段AB的黄金分割点C，并且AC＞CB，AB=1，那么AC的长度为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{3 - \sqrt{5}}{2}$

查看试题解析
3. 二次函数y=x²+2x+3的定义域为（）

A、x＞0 B、x为一切实数 C、y＞2 D、y为一切实数

查看试题解析
4. 已知非零向量 $\vec{a}$ 、 $\vec{b}$ 之间满足 $\vec{a}$ =﹣3 $\vec{b}$ ，下列判断正确的是（）

A、 $\vec{a}$ 的模为3 B、 $\vec{a}$ 与 $\vec{b}$ 的模之比为﹣3：1 C、 $\vec{a}$ 与 $\vec{b}$ 平行且方向相同 D、 $\vec{a}$ 与 $\vec{b}$ 平行且方向相反

查看试题解析
5. 如果从甲船看乙船，乙船在甲船的北偏东30°方向，那么从乙船看甲船，甲船在乙船的（　　）

A、南偏西30°方向 B、南偏西60°方向 C、南偏东30°方向 D、南偏东60°方向

查看试题解析
6. 二次函数y=a（x+m）²+n的图像如图，则一次函数y=mx+n的图像经过（）

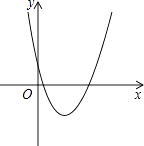A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限

查看试题解析

二、填空题

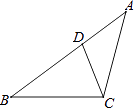
7. 已知2a=3b，则 $\frac{a}{b}$ = ．

查看试题解析
8. 如果两个相似三角形的相似比为1：4，那么它们的面积比为．

查看试题解析
9. 如图，D为△ABC的边AB上一点，如果∠ACD=∠ABC时，那么图中是AD和AB的比例中项．

查看试题解析
10. 如图，△ABC中∠C=90°，若CD⊥AB于D，且BD=4，AD=9，则tanA= ．

查看试题解析
11. 计算：2（ $\vec{a}$ +3 $\vec{b}$ ）﹣5 $\vec{b}$ = ．

查看试题解析
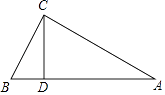12. 如图，G为△ABC的重心，如果AB=AC=13，BC=10，那么AG的长为

查看试题解析
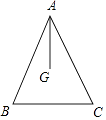13. 二次函数y=5（x﹣4）²+3向左平移二个单位长度，再向下平移一个单位长度，得到的函数解析式是．

查看试题解析
14. 如果点A（1，2）和点B（3，2）都在抛物线y=ax²+bx+c的图像上，那么抛物线y=ax²+bx+c的对称轴是直线．

查看试题解析
15. 已知A（2，y₁）、B（3，y₂）是抛物线y=﹣ $\sqrt{2}$ （x﹣1）²+ $\sqrt{3}$ 的图像上两点，则y₁y₂ ．（填不等号）

查看试题解析
16. 如果在一个斜坡上每向上前进13米，水平高度就升高了5米，则该斜坡的坡度i=

查看试题解析
17. 数学小组在活动中继承了学兄学姐们的研究成果，将能够确定形如y=ax²+bx+c的抛物线的形状、大小、开口方向、位置等特征的系数a、b、c称为该抛物线的特征数，记作：特征数{a、b、c}，（请你求）在研究活动中被记作特征数为{1、﹣4、3}的抛物线的顶点坐标为

查看试题解析
18. 如图，D为直角△ABC的斜边AB上一点，DE⊥AB交AC于E，如果△AED沿DE翻折，A恰好与B重合，联结CD交BE于F，如果AC═8，tanA═ $\frac{1}{2}$ ，那么CF：DF═

查看试题解析

三、解答题

19. 计算： $\frac{\cot 45^{0}}{\tan 60^{0} - 2 \sin 45^{0}}$ ﹣cos30°+（2017﹣π）⁰ ．

查看试题解析
20.
如图，在△ABC中，点D、E分别在边AB、AC上，如果DE∥BC，且DE= $\frac{2}{3}$ BC．

(1)、如果AC=6，求CE的长；

(2)、设 $\vec{A B}$ = $\vec{a}$ ， $\vec{A C}$ = $\vec{b}$ ，求向量 $\vec{D E}$ （用向量 $\vec{a}$ 、 $\vec{b}$ 表示）．

查看试题解析
21. 如图，AB、CD分别表示两幢相距36米的大楼，高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°，观察AB大楼的顶部A点的仰角为30°，求大楼AB的高．

查看试题解析
22. 直线l：y=﹣ $\frac{3}{4}$ x+6交y轴于点A，与x轴交于点B，过A、B两点的抛物线m与x轴的另一个交点为C，（C在B的左边），如果BC=5，求抛物线m的解析式，并根据函数图象指出当m的函数值大于0的函数值时x的取值范围．

查看试题解析
23. 如图，点E是正方形ABCD的对角线AC上的一个动点（不与A、C重合），作EF⊥AC交边BC于点F，联结AF、BE交于点G．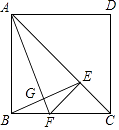

(1)、求证：△CAF∽△CBE；

(2)、若AE：EC=2：1，求tan∠BEF的值．

查看试题解析
24. 如图，二次函数y=ax²﹣ $\frac{3}{2}$ x+2（a≠0）的图像与x轴交于A、B两点，与y轴交于点C，已知点A（﹣4，0）．

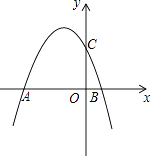(1)、求抛物线与直线AC的函数解析式；

(2)、若点D（m，n）是抛物线在第二象限的部分上的一动点，四边形OCDA的面积为S，求S关于m的函数关系；

(3)、若点E为抛物线上任意一点，点F为x轴上任意一点，当以A、C、E、F为顶点的四边形是平行四边形时，请直接写出满足条件的所有点E的坐标．

查看试题解析
25.
如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm² ．已知y与t的函数关系图像如图（2）（其中曲线OG为抛物线的一部分，其余各部分均为线段）．

(1)、试根据图（2）求0＜t≤5时，△BPQ的面积y关于t的函数解析式；

(2)、求出线段BC、BE、ED的长度；

(3)、当t为多少秒时，以B、P、Q为顶点的三角形和△ABE相似；

(4)、如图（3）过E作EF⊥BC于F，△BEF绕点B按顺时针方向旋转一定角度，如果△BEF中E、F的对应点H、I恰好和射线BE、CD的交点G在一条直线，求此时C、I两点之间的距离．

查看试题解析