2016年内蒙古呼和浩特市中考数学一模试卷
试卷更新日期:2017-02-22 类型:中考模拟
一、选择题
-
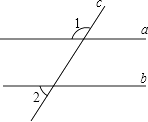
1. 方程﹣2x+3=0的解是( )A、 B、﹣ C、 D、﹣2. 已知:如图,直线a∥b,直线c与直线a、b相交.∠1=120°,则∠2的度数是( )
 A、120° B、60° C、30° D、80°3. 一个圆锥侧面展开图的扇形的弧长为12π,则这个圆锥底面圆的半径为( )A、6 B、12 C、24 D、24. 若a>0且ax=2,ay=3,则ax﹣2y的值为( )A、 B、﹣ C、 D、5. 如图是几何体的三视图,根据图中数据,求得该几何体的体积为( )
A、120° B、60° C、30° D、80°3. 一个圆锥侧面展开图的扇形的弧长为12π,则这个圆锥底面圆的半径为( )A、6 B、12 C、24 D、24. 若a>0且ax=2,ay=3,则ax﹣2y的值为( )A、 B、﹣ C、 D、5. 如图是几何体的三视图,根据图中数据,求得该几何体的体积为( )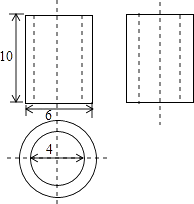 A、40π B、50π C、90π D、130π6. 在数轴上任取一个比﹣5大比7小的实数a对应的点,则取到的点对应的实数a满足|a|>2的概率为( )A、 B、 C、 D、7. 函数y=ax﹣2(a≠0)与y=ax2(a≠0)在同一平面直角坐标系中的图像可能是( )A、
A、40π B、50π C、90π D、130π6. 在数轴上任取一个比﹣5大比7小的实数a对应的点,则取到的点对应的实数a满足|a|>2的概率为( )A、 B、 C、 D、7. 函数y=ax﹣2(a≠0)与y=ax2(a≠0)在同一平面直角坐标系中的图像可能是( )A、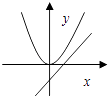 B、
B、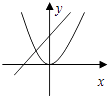 C、
C、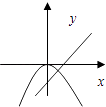 D、
D、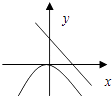 8. 数轴上表示1,的对应点分别为A、B.点B关于点A的对称点为C,则点C所表示的相反数是( )A、﹣1﹣ B、1﹣ C、﹣2+ D、﹣2﹣9. 下列运算正确的是( )A、 × = B、 • =1 C、﹣2x2﹣3x+5=(1﹣x)(2x+5) D、(﹣a)7÷a3=a410. 以下四个函数,其图像一定关于原点对称的是( )A、y=2016x+m B、y= + C、y=x2﹣2016 D、y=
8. 数轴上表示1,的对应点分别为A、B.点B关于点A的对称点为C,则点C所表示的相反数是( )A、﹣1﹣ B、1﹣ C、﹣2+ D、﹣2﹣9. 下列运算正确的是( )A、 × = B、 • =1 C、﹣2x2﹣3x+5=(1﹣x)(2x+5) D、(﹣a)7÷a3=a410. 以下四个函数,其图像一定关于原点对称的是( )A、y=2016x+m B、y= + C、y=x2﹣2016 D、y=二、填空题
-
11. 已知某孢子的直径为0.00093毫米,用科学记数法写为毫米.12. 北偏东30°与南偏东50°的两条射线组成的角的度数为°.
13. 顺次连接A,B,C,D得到平行四边形ABCD,已知AB=4,BC=6,∠B=60°.则此平行四边形面积是 .14. 用换元法解分式方程 ﹣ =﹣1时,如果设 =y,并将原方程化为关于y的整式方程,那么这个整式方程是15. 腰长为10,一条高为8的等腰三角形的底边长为 .16. 以下四个命题:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形:②两条对角线互相垂直且相等的四边形是正方形:③一组数据2,4,6.4的方差是2;④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.点A、C在第一象限.若点D坐标为(2 ,0),则点A坐标为( , ),其中正确命题有(填正确命题的序号即可)三、解答题
-
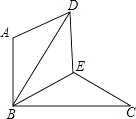
17. 化简求值与计算(1)、先化简,再求值.( + )•(x2﹣1),其中x= .(2)、计算:|4﹣ |﹣( ﹣ )× +( )﹣1 .18. 如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
 (1)、求证:△BDE≌△BCE;(2)、试判断四边形ABED的形状,并说明理由.19. 某微商一次购进了一种时令水果250千克,开始两天他以每千克高于进价40%的价格卖出180千克.第三天他发现网上卖该种水果的商家陡增,于是他果断将剩余的该种水果在前两天的售价基础上打4折全部售出.最后他卖该种水果获得618元的利润,计算商家打折卖出的该种剩余水果亏了多少元?20. 已知关于x的不等式组 (a≠0)求该不等式组的解集.21. 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).
(1)、求证:△BDE≌△BCE;(2)、试判断四边形ABED的形状,并说明理由.19. 某微商一次购进了一种时令水果250千克,开始两天他以每千克高于进价40%的价格卖出180千克.第三天他发现网上卖该种水果的商家陡增,于是他果断将剩余的该种水果在前两天的售价基础上打4折全部售出.最后他卖该种水果获得618元的利润,计算商家打折卖出的该种剩余水果亏了多少元?20. 已知关于x的不等式组 (a≠0)求该不等式组的解集.21. 如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).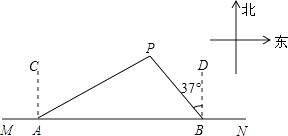 22. 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
22. 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: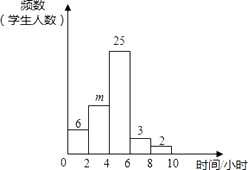 (1)、求m的值;(2)、计算50名学生的课外活动时间的平均数(每组时间用其组中值表示),对初三年级全体学生平均每周的课外活动时间做个推断;(3)、从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表法,求其中至少有1人课外活动时间在8~10小时的概率.23. 如图,在平面直角坐标系中,一次函数y=kx+b的图像分別交x轴、y轴于A、B两点.与反比例函数y=﹣ 的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
(1)、求m的值;(2)、计算50名学生的课外活动时间的平均数(每组时间用其组中值表示),对初三年级全体学生平均每周的课外活动时间做个推断;(3)、从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表法,求其中至少有1人课外活动时间在8~10小时的概率.23. 如图,在平面直角坐标系中,一次函数y=kx+b的图像分別交x轴、y轴于A、B两点.与反比例函数y=﹣ 的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.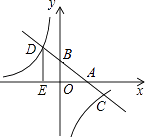 (1)、求一次函数的解析式;(2)、直接写出不等式kx+b+ >0的解集.24. 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.
(1)、求一次函数的解析式;(2)、直接写出不等式kx+b+ >0的解集.24. 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.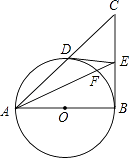 (1)、求证:E是BC的中点;(2)、求证:AD•AC=AE•AF=4DO2 .25. 如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).
(1)、求证:E是BC的中点;(2)、求证:AD•AC=AE•AF=4DO2 .25. 如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).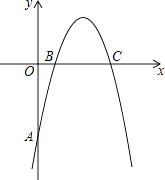 (1)、求此抛物线的解析式;(2)、记抛物线的顶点为M,求△ACM的面积;(3)、在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求此抛物线的解析式;(2)、记抛物线的顶点为M,求△ACM的面积;(3)、在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.