2016年湖北省十堰市中考数学一模试卷

试卷更新日期：2017-02-22 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列实数中，是无理数的为（）

A、﹣1 B、﹣ $\frac{1}{2}$ C、 $\sqrt{2}$ D、3.14

查看试题解析
2. 如图，l∥m，等边△ABC的顶点B在直线m上，∠1=20°，则∠2的度数为（）

A、60° B、45° C、40° D、30°

查看试题解析
3. 如图所示几何体的俯枧图是（）

A、 B、 C、 D、

查看试题解析
4. 若（m﹣1）²+ $\sqrt{n + 2}$ =0，则m+n的值是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
5. 甲、乙、丙、丁四人一起到冰店买红豆与桂圆两种棒冰．四人购买的数量及总价分别如表所示．若其中一人的总价算错了，则此人是谁（）
甲
乙
丙
丁
红豆棒冰（枝）
18
15
24
27
桂圆棒冰（枝）
30
25
40
45
总价（元）
396
330
528
585

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 如图，已知一张纸片▱ABCD，∠B＞90°，点E是AB的中点，点G是BC上的一个动点，沿BG将纸片折叠，使点B落在纸片上的点F处，连接AF，则下列各角中与∠BEG不一定相等的是（）

A、∠FEG B、∠EAF C、∠AEF D、∠EFA

查看试题解析
7. 如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为（）

A、5cm B、6cm C、7cm D、8cm

查看试题解析
8.
同样大小的黑色棋子按如图所示的规律摆放：
那么第671个图形中棋子的个数为（）

A、2016 B、2015 C、2014 D、2013

查看试题解析
9.
如图，已知A，B是反比例函数y= $\frac{k}{x}$ （k＞0，x＞0）图像上的两点，BC∥x轴，交y轴于点C，动点P纵坐标原点O出发，沿O→A→B→C匀速运动，终点为C，过点P作PM⊥x轴，PN⊥y轴，垂足分别为M，N．设四边形OMPN的面积为S，点P运动的时间为t，则S关于t的函数图象大致为（）

A、 B、 C、 D、

查看试题解析
10. 图1是一个八角星形纸板，图中有八个直角、八个相等的钝角，每条边都相等，如图2将纸板沿虚线进行切割，无缝隙无重叠的拼成如图3所示的大正方形，其面积为8+4 $\sqrt{2}$ ，则图3中线段AB的长为（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、 $\sqrt{2}$ ﹣1 D、 $\sqrt{2}$ +1

查看试题解析

二、填空题

11. 据第六次全国人口普查统计，我国人口总数约有1 370 000 000人，用科学记数法表示为人．

查看试题解析
12. 如图，要使输出值y大于100，则输入的最小正整数x是．

查看试题解析
13. 我市某体育用品商店购进了一批运动服，每件售价120元，可获利20%，这种衣服每件的进价是元．

查看试题解析
14. 如图，直线l与⊙O交于C，D两点，且与半径OA垂直，垂足为H，∠ODC=30°，在OD的延长线上取一点B，使得AD=BD，若⊙O的半径为2，则图中阴影部分的面积为（结果保留π）

查看试题解析
15. 如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°方向的C地有一艘渔船遇险，要求马上前去救援，要求马上前去救援．此时C地位于A地北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之间的距离为12海里，则A、C两地之间的距离为．

查看试题解析
16.
如图所示，直线AB与x轴交于点A，与y轴交于点B，点A的坐标为（3，0），点B的坐标为（0，4），点P为双曲线y= $\frac{6}{x}$ （x＞0）上的一点，过点P分别作x轴、y轴的垂线段PE、PF，当PE、PF分别与线段AB交于点C、D时，AD•BC的值为

查看试题解析

三、解答题

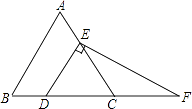
17. 化简，求值： $\frac{m^{2} - 2 m + 1}{m^{2} - 1} \div (m - 1 - \frac{m - 1}{m + 1})$ ，其中m= $\sqrt{3}$ ．

查看试题解析
18. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．

(1)、求∠F的度数；

(2)、若CD=2，求DF的长．

查看试题解析
19. 为改善生态环境，防止水土流失，某村计划在荒坡上种1000棵树．由于青年志愿者的支援，每天比原计划多种25%，结果提前5天完成任务，原计划每天种多少棵树？

查看试题解析
20. 为更好地宣传“开车不喝酒，喝酒不开车”的驾车理念，某市一家报社设计了如图的调查问卷（单选）．在随机调查了某市全部5 000名司机中的部分司机后，统计整理并制作了如下的统计图：
根据以上信息解答下列问题：

(1)、补全条形统计图，并计算扇形统计图中m=；

(2)、该市支持选项B的司机大约有多少人？

(3)、若要从该市支持选项B的司机中随机选择100名，给他们发放“请勿酒驾”的提醒标志，则支持该选项的司机小李被选中的概率是多少？

查看试题解析
21. 已知关于x的一元二次方程x²+（2m﹣1）x+m²=0有两个实数根x₁和x₂ ．

(1)、求实数m的取值范围；

(2)、当x₁²﹣x₂²=0时，求m的值．

查看试题解析
22. 如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．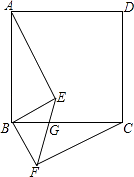

(1)、求证：AE=CF；

(2)、若∠ABE=55°，求∠EGC的大小．

查看试题解析
23. 大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
x（天）
1
2
3
…
50
p（件）
118
116
114
…
20
销售单价q（元/件）与x满足：当1≤x＜25时q=x+60；当25≤x≤50时q=40+ $\frac{1125}{x}$ ．

(1)、请分析表格中销售量p与x的关系，求出销售量p与x的函数关系．

(2)、求该超市销售该新商品第x天获得的利润y元关于x的函数关系式．

(3)、这50天中，该超市第几天获得利润最大？最大利润为多少？

查看试题解析
24. 如图，AB是⊙O的直径，点C，D是半圆O的三等分点，过点C作⊙O的切线交AD的延长线于点E，过点D作DF⊥AB于点F，交⊙O于点H，连接DC，AC．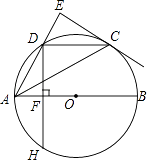

(1)、求证：∠AEC=90°；

(2)、试判断以点A，O，C，D为顶点的四边形的形状，并说明理由；

(3)、若DC=2，求DH的长．

查看试题解析
25.
如图，在平面直角坐标系中，直线y=﹣3x﹣3与x轴交于点A，与y轴交于点C．抛物线y=x²+bx+c经过A，C两点，且与x轴交于另一点B（点B在点A右侧）．

(1)、求抛物线的解析式及点B坐标；

(2)、若点M是线段BC上一动点，过点M的直线EF平行y轴交x轴于点F，交抛物线于点E．求ME长的最大值；

(3)、试探究当ME取最大值时，在x轴下方抛物线上是否存在点P，使以M，F，B，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由．

查看试题解析

	甲	乙	丙	丁
红豆棒冰（枝）	18	15	24	27
桂圆棒冰（枝）	30	25	40	45
总价（元）	396	330	528	585

x（天）	1	2	3	…	50
p（件）	118	116	114	…	20