2016年安徽省巢湖市庐江县中考数学一模试卷
试卷更新日期:2017-02-22 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、0 B、1 C、﹣1 D、﹣2. 计算(﹣2x2)3的结果是( )A、﹣2x5 B、﹣8x6 C、﹣2x6 D、﹣8x53.
如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )
 A、
A、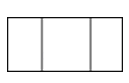 B、
B、 C、
C、 D、
D、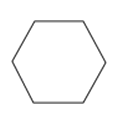 4. 下面调查中,适合采用普查的是( )A、调查全国中学生心理健康现状 B、调查你所在的班级同学的身高情况 C、调查我市食品合格情况 D、调查南京市电视台《今日生活》收视率5. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于( )
4. 下面调查中,适合采用普查的是( )A、调查全国中学生心理健康现状 B、调查你所在的班级同学的身高情况 C、调查我市食品合格情况 D、调查南京市电视台《今日生活》收视率5. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于( ) A、70° B、65° C、80° D、35°6. 若点P1(x1 , y1),P2(x2 , y2)在反比例函数y= (k>0)的图像上,且x1=﹣x2 , 则( )A、y1<y2 B、y1=y2 C、y1>y2 D、y1=﹣y27. 某书每本定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,超过10本部分按八折付款.设一次购书数量为x本(x>10),则付款金额为( )A、6.4x元 B、(6.4x+80)元 C、(6.4x+16)元 D、(144﹣6.4x)元8. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A、70° B、65° C、80° D、35°6. 若点P1(x1 , y1),P2(x2 , y2)在反比例函数y= (k>0)的图像上,且x1=﹣x2 , 则( )A、y1<y2 B、y1=y2 C、y1>y2 D、y1=﹣y27. 某书每本定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,超过10本部分按八折付款.设一次购书数量为x本(x>10),则付款金额为( )A、6.4x元 B、(6.4x+80)元 C、(6.4x+16)元 D、(144﹣6.4x)元8. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) A、2 B、8 C、 D、29. 求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016 , 于是2S=2+22+23+…+22017 , 因此2S﹣S=22017﹣1,所以S=22017﹣1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )A、52017﹣1 B、52016﹣1 C、 D、10. 如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图像是( )
A、2 B、8 C、 D、29. 求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016 , 于是2S=2+22+23+…+22017 , 因此2S﹣S=22017﹣1,所以S=22017﹣1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )A、52017﹣1 B、52016﹣1 C、 D、10. 如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图像是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 2015年,合肥市户籍人口数约为801.4万人,将801.4万用科学记数法表示应是 .12. 在实数范围内分解因式:x3﹣2x=13. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位后得到△DEF,连接DC,则DC的长为
 14. 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论:
14. 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③∠CDE=∠COD;④2CD2=CE•AB.
其中正确结论的序号是(在横线上填上你认为所有正确结论的代号).

三、解答题
-
15. 计算:﹣12016﹣23÷(﹣2)+(﹣ )0﹣ .16. 解不等式组 并把解集在数轴上表示出来.17. 每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.

(I)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1 , 请画出菱形OA1B1C1 , 并直接写出点B1的坐标;
(II)将菱形OABC绕原点O顺时针旋转90°菱形OA2B2C2 , 请画出菱形OA2B2C2 , 并求出点B旋转到点B2的路径长.
18. 如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证:①△ABM≌△CBM;
②CG⊥CM.
 19. 张明3h清点完一批图书的一半,李强加入清点另一半图书的工作,两人合作1.2h清点完另一半图书.哪个人清点速度快?20. “端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
19. 张明3h清点完一批图书的一半,李强加入清点另一半图书的工作,两人合作1.2h清点完另一半图书.哪个人清点速度快?20. “端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)、本次参加抽样调查的居民有多少人?(2)、将两幅不完整的图补充完整;(3)、若居民区有8000人,请估计爱吃D粽的人数;(4)、若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.21. 如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求: (1)、tanC;(2)、图中两部分阴影面积的和.22. 如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)、tanC;(2)、图中两部分阴影面积的和.22. 如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C. (1)、求抛物线的函数解析式;(2)、连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF.23. 如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
(1)、求抛物线的函数解析式;(2)、连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF.23. 如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.
 (1)、小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).(2)、小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.(3)、若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”.
(1)、小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).(2)、小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.(3)、若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”.