2015-2016学年湖北省重点高中联考协作体高三下学期期中数学试卷（理科）

试卷更新日期：2017-02-22 类型：期中考试

进入出卷网下载

一、选择题

1. 复数 $\frac{2 + i}{1 - 2 i}$ 的共轭复数是（）

A、- $\frac{3}{5} i$ B、 $\frac{3}{5} i$ C、﹣i D、i

查看试题解析
2. “x＜0”是“ln（x+1）＜0”的（　　）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 已知集合A={1，2，3，4，5}，B={（x，y）|x∈A，y∈A，x﹣y∈A}，则B中所含元素的个数为（　　）

A、3 B、6 C、8 D、10

查看试题解析
4. 某产品的广告费用x与销售额y的统计数据如表：
广告费用x（万元）
4
2
3
5
销售额y（万元）
49
26
39
54
根据上表可得回归方程 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ 中的 $\hat{b}$ 为9.4，据此模型预报广告费用为6万元时销售额为（）

A、63.6万元 B、67.7万元 C、65.5万元 D、72.0万元

查看试题解析
5. 为得到函数y=cos（2x+ $\frac{π}{3}$ ）的图像，只需将函数y=sin2x的图像（）

A、向左平移 $\frac{5 π}{12}$ 个单位长度 B、向右平移 $\frac{5 π}{12}$ 个单位长度 C、向左平移 $\frac{5 π}{6}$ 个单位长度 D、向右平移 $\frac{5 π}{6}$ 个单位长度

查看试题解析
6. 已知等差数列{a_n}的前n项和为S_n ， a₅=5，S₅=15，则数列 ${\frac{1}{a_{n} a_{n + 1}}}$ 的前100项和为（）

A、 $\frac{100}{101}$ B、 $\frac{99}{101}$ C、 $\frac{99}{100}$ D、 $\frac{101}{100}$

查看试题解析
7. （x+ $\frac{a}{x}$ ）（2x﹣ $\frac{1}{x}$ ）⁵的展开式中各项系数的和为2，则该展开式中常数项为（）

A、﹣40 B、﹣20 C、20 D、40

查看试题解析
8. 从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离不小于该正方形边长的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 执行下面的程序框图，如果输入的t=0.01，则输出的n=（）

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为（）

A、6 $\sqrt{2}$ B、4 $\sqrt{2}$ C、6 D、4

查看试题解析
11. 已知A，B为双曲线E的左，右顶点，点M在E上，△ABM为等腰三角形，顶角为120°，则E的离心率为（）

A、 $\sqrt{5}$ B、2 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
12. 设函数f（x）= $\sqrt{3}$ sin $\frac{π x}{m}$ ，若存在f（x）的极值点x₀满足x₀²+[f（x₀）]²＜m² ，则m的取值范围是（）

A、（﹣∞，﹣6）∪（6，+∞） B、（﹣∞，﹣4）∪（4，+∞） C、（﹣∞，﹣2）∪（2，+∞） D、（﹣∞，﹣1）∪（1，+∞）

查看试题解析

二、填空题

13. 设x，y满足约束条件： ${\begin{matrix} x \geq 0 ， y \geq 0 \\ x - y \geq - 1 \\ x + y \leq 3 \end{matrix}$ ；则z=x﹣2y的取值范围为．

查看试题解析
14. 函数f（x）=log₂ $\sqrt{x}$ •log $_{\sqrt{2}}$ （2x）的最小值为．

查看试题解析
15. 从班委会5名成员中选出3名，分别担任班级学习委员、文娱委员与体育委员，其中甲、乙二人不能担任文娱委员，则不同的选法共有种．（用数字作答）

查看试题解析
16. 平面向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{e}$ 满足| $\vec{e}$ |=1， $\vec{a}$ • $\vec{e}$ =1， $\vec{b}$ • $\vec{e}$ =2，| $\vec{a}$ ﹣ $\vec{b}$ |=2，则 $\vec{a}$ • $\vec{b}$ 的最小值为．

查看试题解析

三、解答题

17. 已知 $\vec{a}$ =（sinx，sin（x﹣ $\frac{π}{6}$ ））， $\vec{b}$ =（sinx，cos（x+ $\frac{π}{3}$ ）），f（x）= $\vec{a}$ • $\vec{b}$ ．

(1)、求f（x）的解析式及周期；

(2)、求f（x）在x∈[﹣ $\frac{π}{3}$ ， $\frac{π}{4}$ ]上的值域．

查看试题解析
18. 双“十一”结束之后，某网站针对购物情况进行了调查，参与调查的人主要集中在[20，50]岁之间，若规定：购物600（含600元）以下者，称为“理智购物”，购物超过600元者被网友形象的称为“剁手党”，得到如下统计表：
分组编号
年龄分组
球迷
所占比例
1
[20，25）
1000
0.5
2
[25，30）
1800
0.6
3
[30，35）
1200
0.5
4
[35，40）
a
0.4
5
[40，45）
300
0.2
6
[45，50]
200
0.1
若参与调查的“理智购物”总人数为7720人．

(1)、求a的值；

(2)、从年龄在[20，35）的“剁手党”中按照年龄区间分层抽样的方法抽取20人；
①从这20人中随机抽取2人，求这2人恰好属于同一年龄区间的概率；
②从这20人中随机抽取2人，用ζ表示年龄在[20，25）之间的人数，求ξ的分布列及期望值．

查看试题解析
19. 如图，在四棱锥P﹣ABCD中，AD∥BC，AB⊥AD，AB⊥PA，BC=2AB=2AD=4BE，平面PAB⊥平面ABCD，
（Ⅰ）求证：平面PED⊥平面PAC；
（Ⅱ）若直线PE与平面PAC所成的角的正弦值为 $\frac{\sqrt{5}}{5}$ ，求二面角A﹣PC﹣D的平面角的余弦值．

查看试题解析
20. 如图已知椭圆C： $\frac{x^{2}}{4}$ +y²=1，以椭圆的左顶点T为圆心作圆T：（x+2）²+y²=r²（r＞0）．设圆T与椭圆C交于点M与点N．

(1)、求 $\vec{T M} \cdot \vec{T N}$ 的最小值；

(2)、设点P是椭圆C上异于M，N的任意一点，且直线MP，NP分别与x轴交于点R，S，O为坐标原点，求证：丨OR丨•丨OS丨为定值．

查看试题解析
21. 已知函数f（x）=x（lnx﹣ax）．

(1)、a= $\frac{1}{2}$ 时，求f（x）在点（1，f（1））处的切线方程；

(2)、若f（x）存在两个不同的极值x₁ ， x₂ ，求a的取值范围；

(3)、在（2）的条件下，求f（x）在（0，a]上的最小值．

查看试题解析
22. 如图，点A是以线段BC为直径的圆O上一点，AD⊥BC于点D，过点B作圆O的切线，与CA的延长线相交于点E，点G是AD的中点，连接CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．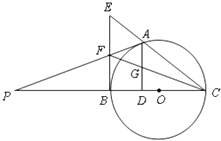

(1)、求证：BF=EF；

(2)、求证：PA是圆O的切线．

查看试题解析
23. 在极坐标系下，已知圆O：ρ=cosθ+sinθ和直线l：ρsin（θ﹣ $\frac{π}{4}$ ）= $\frac{\sqrt{2}}{2}$ ．

(1)、求圆O和直线l的直角坐标方程；

(2)、当θ∈（0，π）时，求直线l与圆O公共点的极坐标．

查看试题解析
24. 已知f（x）=|ax+1|（a∈R），不等式f（x）≤3的解集为{x|﹣2≤x≤1}．
（Ⅰ）求a的值；
（Ⅱ）若f（x）﹣2f（ $\frac{x}{2}$ ）≤k恒成立，求k的取值范围．

查看试题解析

分组编号	年龄分组	球迷	所占比例
1	[20，25）	1000	0.5
2	[25，30）	1800	0.6
3	[30，35）	1200	0.5
4	[35，40）	a	0.4
5	[40，45）	300	0.2
6	[45，50]	200	0.1

广告费用x（万元）	4	2	3	5
销售额y（万元）	49	26	39	54