2018-2019学年数学浙教版九年级上册1.3 二次函数的性质 同步练习
试卷更新日期：2018-08-15 类型：同步测试
一、选择题
-
1. 已知抛物线 ，则下列关于最值叙述正确的是（ ）
A、函数有最小值是3 B、函数有最大值是3 C、函数有最小值是 D、函数有最大值是2. 二次函数y=x2﹣8x+1的最小值是（ ）
A、4 B、﹣15 C、﹣4 D、153. 当二次函数y＝x2＋4x＋9取最小值时，x的值为（ ）
A、－2 B、1 C、2 D、94. 在二次函数y＝x2－2x－3中，当0≤x≤3时，y的最大值和最小值分别是 （ ）
A、0，－4 B、0，－3 C、－3，－4 D、0，05. 抛物线 与坐标轴的交点个数是（ ）A、3 B、2 C、1 D、06. 二次函数 的图象如图所示，那么一元二次方程 为常数且 的两根之和为 （ ）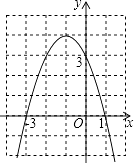
A、1 B、2 C、-1 D、-27. 已知抛物线y＝(a＋1)x2－ax－8，过点（2，－2），且与x轴的一个交点的横坐标为2n，则代数式4n2－n＋2016 的值为（ ）A、2020 B、2019 C、2018 D、20178. 下列二次函数的图象与x轴有两个不同的交点的是（ ）
A、y=x2 B、y=x2+4 C、y=3x2﹣2x+5 D、y=3x2+5x﹣19. 某鞋帽专卖店销售一种绒帽，若这种帽子每天获利y（元）与销售单价x（元）满足关系y=﹣x2+70x﹣800，要想获得最大利润，则销售单价为（ ）
A、30元 B、35元 C、40元 D、45元10. 二次函数y=﹣x2+6x﹣7，当x取值为t≤x≤t+2时，y最大值=﹣（t﹣3）2+2，则t的取值范围是（）A、t=0 B、0≤t≤3 C、t≥3 D、以上都不对二、填空题
-
11. 若二次函数y=x2－bx+1的图像与x轴只有一个交点，则b的值是 ．
12. 已知二次函数y＝2x2－6x＋1，当0≤x≤5时，y的取值范围是 ．
13. 一位运动员投掷铅球，如果铅球运行时离地面的高度为y（米）关于水平距离x（米）的函数解析式为y=﹣ ，那么铅球运动过程中最高点离地面的距离为米．
14. 已知二次函数 ，当 时， 的最大值为5，则实数 的值为.
15. 如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x﹣m）2+n的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为﹣3，则点D的横坐标最大值为 ．
三、解答题
-
16. 向上抛掷一个小球，小球在运行过程中，离地面的距离为y(m)，运行时间为x(s)，y与x之间存在的关系为y＝－ x2＋3x＋2.问：小球能达到的最大高度是多少？
17. 当k分别取0，1时，函数y＝(1－k)x2－4x＋5－k都有最小值吗？写出你的判断，并说明理由．18. 已知点P（﹣1，n）和Q（3，n）都在二次函数y=x2+bx﹣1的图象上．
(1)、求b、n的值；(2)、将二次函数图象向上平移几个单位后，得到的图象与x轴只有一个公共点？
19. 随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y1（单位：分钟）是关于x的一次函数，其关系如下表：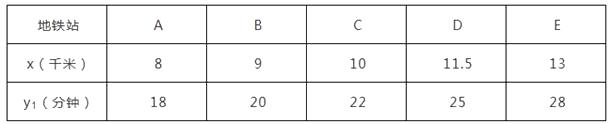
(1)、求y1关于x的函数表达式；
(2)、李华骑单车的时间（单位：分钟）也受x的影响，其关系可以用y2=x2-11x+78来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．
20. 在平面直角坐标系xOy中，抛物线y=ax2﹣4ax+3a（a＞0）与x轴交于A，B两点（A在B的左侧）．
(1)、求抛物线的对称轴及点A，B的坐标；(2)、点C（t，3）是抛物线y=ax2﹣4ax+3a（a＞0）上一点，（点C在对称轴的右侧），过点C作x轴的垂线，垂足为点D．①当CD=AD时，求此时抛物线的表达式；
②当CD＞AD时，求t的取值范围．
21. 已知：关于x的函数y=kx2+k2x﹣2的图象与y轴交于点C，
(1)、当k=﹣2时，求图象与x轴的公共点个数；(2)、若图象与x轴有一个交点为A，当△AOC是等腰三角形时，求k的值．(3)、若x≥1时函数y随着x的增大而减小，求k的取值范围．