2018-2019学年数学浙教版九年级上册1.2 二次函数的图象(3) 同步练习
试卷更新日期:2018-08-15 类型:同步测试
一、选择题
-
1. 抛物线y=x2﹣2x+1的顶点坐标是( )
A、(1,0) B、(﹣1,0) C、(﹣2,1) D、(2,﹣1)2. 抛物线 的对称轴是( )A、直线x=1 B、直线x= -1 C、直线x=-2 D、直线x=23. 若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A、﹣1 B、0 C、1 D、24. 二次函数y=x2+2x+3的图象的开口方向为( )
A、向上 B、向下 C、向左 D、向右5. 抛物线y=﹣ x2+ x﹣1,经过配方化成y=a(x﹣h)2+k的形式是( )A、 B、 C、 D、6. 如图,老师出示了小黑板上的题后,小华添加的条件是过点(3,0);小彬添加的条件是过点(4,3);小明添加的条件是a=1;小颖添加的条件是抛物线被x轴截得的线段长为2.你认为四人添加的条件中,正确的有( ) A、1个 B、2个 C、3个 D、4个7. 如图,已知二次函数 的部分图象与坐标轴交于A(3,0)和C(0,2)两点,对称轴为直线 ,当函数值 >0时,自变量 的取值范围是( )
A、1个 B、2个 C、3个 D、4个7. 如图,已知二次函数 的部分图象与坐标轴交于A(3,0)和C(0,2)两点,对称轴为直线 ,当函数值 >0时,自变量 的取值范围是( )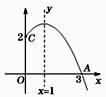 A、 <3 B、0≤ <3 C、-2< <3 D、-1< <38. 二次函数 在 的范围内有最小值 ,则 的值是( )
A、 <3 B、0≤ <3 C、-2< <3 D、-1< <38. 二次函数 在 的范围内有最小值 ,则 的值是( )
A、 B、 C、 D、9. 为了得到函数y=3x2的图象,可以将函数y=﹣3x2﹣6x﹣1的图象( )A、先关于x轴对称,再向右平移1个单位,最后向上平移2个单位 B、先关于x轴对称,再向右平移1个单位,最后向下平移2个单位 C、先关于y轴对称,再向右平移1个单位,最后向上平移2个单位 D、先关于y轴对称,再向右平移1个单位,最后向下平移2个单位10. 如图,在平面直角坐标系中,边长为 的正方形 的边 轴,顶点 的坐标为 .二次函数 的图象的顶点在正方形 的边上运动,则 的值可以( ).
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式3﹣a﹣b的值为 .
12. 抛物线 的顶点坐标是 , 对称轴是.13. 已知抛物线y=3x2﹣4x+c的顶点在x轴上方,则c应满足的条件 .
14. 已知抛物线y=(x﹣2)2﹣3的部分图象如图所示,若y≤0,则x的取值范围为 . 15. 如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是.
15. 如图,已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是.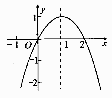 16. 已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 . (写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
16. 已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 . (写出所有正确结论的序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
三、解答题
-
17. 已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,-3)三点.
(1)、求这条抛物线的解析式;(2)、写出抛物线的开口方向、对称轴和顶点坐标.
18. 已知二次函数y=﹣x2+4x. (1)、写出二次函数y=﹣x2+4x图象的对称轴;(2)、在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(1)、写出二次函数y=﹣x2+4x图象的对称轴;(2)、在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)、根据图象,写出当y<0时,x的取值范围.
19. 对于函数y=﹣x2﹣2x﹣1,请回答下列问题:
(1)、图象的对称轴,顶点坐标各是什么?当x取何值时,函数有最大(小)值,函数最大(小)值是多少?
(2)、求抛物线与x轴的交点,与y轴的交点坐标是什么?
20. 已知函数 的顶点为点D.(1)、求点D的坐标(用含m的代数式表示);(2)、求函数 的图象与x轴的交点坐标;(3)、若函数 的图象在直线y=m的上方,求m的取值范围.
