2018-2019学年数学浙教版九年级上册1.4 二次函数的应用(1) 同步练习
试卷更新日期:2018-08-15 类型:同步测试
一、选择题
-
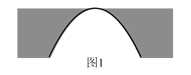
1. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
 A、y= B、y=﹣ C、y=﹣ D、y=2.
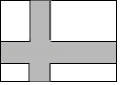
A、y= B、y=﹣ C、y=﹣ D、y=2.如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
 A、32×20﹣20x﹣30x=540 B、32×20﹣20x﹣30x﹣x2=540 C、(32﹣x)(20﹣x)=540 D、32×20﹣20x﹣30x+2x2=5403. 如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A、32×20﹣20x﹣30x=540 B、32×20﹣20x﹣30x﹣x2=540 C、(32﹣x)(20﹣x)=540 D、32×20﹣20x﹣30x+2x2=5403. 如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )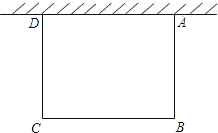 A、10米 B、15米 C、20米 D、25米4. 如图所示是二次函数y= 的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为可能的值是( )
A、10米 B、15米 C、20米 D、25米4. 如图所示是二次函数y= 的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为可能的值是( )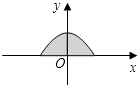 A、4 B、 C、2π D、85. 将抛物线 向右平移 个单位,再向下平移 个单位,得到抛物线 , 与 轴交于 、 两点, 的顶点记为 ,则 的面积为( ).
A、4 B、 C、2π D、85. 将抛物线 向右平移 个单位,再向下平移 个单位,得到抛物线 , 与 轴交于 、 两点, 的顶点记为 ,则 的面积为( ).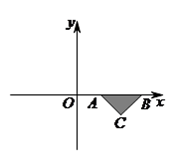 A、 B、 C、 D、6. 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
A、 B、 C、 D、6. 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )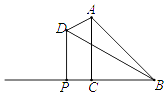 A、一直变大 B、一直变小 C、先变小再变大 D、先变大再变小7. 小明以二次函数y=2x2-4x+8的图象为灵感为“2017北京·房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( )
A、一直变大 B、一直变小 C、先变小再变大 D、先变大再变小7. 小明以二次函数y=2x2-4x+8的图象为灵感为“2017北京·房山国际葡萄酒大赛”设计了一款杯子,如图为杯子的设计稿,若AB=4,DE=3,则杯子的高CE为( )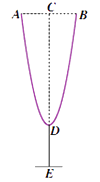 A、14 B、11 C、6 D、3
A、14 B、11 C、6 D、3二、填空题
-
8. 用 的铁丝所围的长方形的面积 与长 的关系 .
9. 如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB间,按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为米.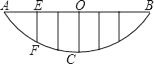 10. 如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线 (a<0)的顶点为D , 且经过点A、B . 若△ABD为等腰直角三角形,则a的值为 .
10. 如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线 (a<0)的顶点为D , 且经过点A、B . 若△ABD为等腰直角三角形,则a的值为 .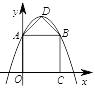 11. 如图,抛物线 与 轴交于点 ,过点 与 轴平行的直线交抛物线 于点 、 ,则线段 的长为.
11. 如图,抛物线 与 轴交于点 ,过点 与 轴平行的直线交抛物线 于点 、 ,则线段 的长为.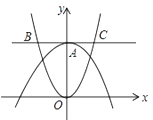 12. 如图,菱形OABC的顶点O、A、C在抛物线 上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是 .
12. 如图,菱形OABC的顶点O、A、C在抛物线 上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是 .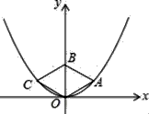 13. 如图,线段 的长为2, 为 上一个动点,分别以 、 为斜边在 的同侧作两个等腰直角三角形 和 ,那么 长的最小值是.
13. 如图,线段 的长为2, 为 上一个动点,分别以 、 为斜边在 的同侧作两个等腰直角三角形 和 ,那么 长的最小值是.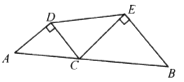
三、解答题
-
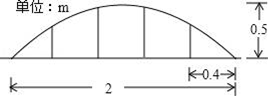
14. 某景区内有一块矩形油菜花田地(数据如图示,单位:m.)
现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.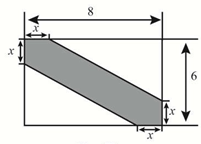 (1)、求y与x的函数表达式;
(1)、求y与x的函数表达式;
(2)、若改造后观花道的面积为13m2 , 求x的值;(3)、若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
15. 有一座抛物线拱型桥,在正常水位时,水面BC的宽为10米,拱桥的最高点D到水面BC的距离DO为4米,点O是BC的中点,如图,以点O为原点,直线BC为x , 建立直角坐标xOy .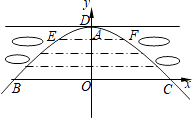 (1)、求该抛物线的表达式;(2)、如果水面BC上升3米 即 至水面EF , 点E在点F的左侧,求水面宽度EF的长.16. 甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.
(1)、求该抛物线的表达式;(2)、如果水面BC上升3米 即 至水面EF , 点E在点F的左侧,求水面宽度EF的长.16. 甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.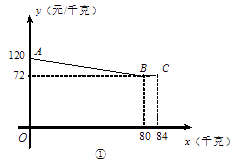
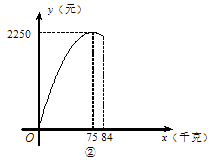 (1)、分别求出图①中线段AB、图②中抛物线所表示的函数表达式;(2)、当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
(1)、分别求出图①中线段AB、图②中抛物线所表示的函数表达式;(2)、当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?