2016-2017学年浙江省温州市平阳二中高三上学期期中数学试卷
试卷更新日期:2017-02-21 类型:期中考试
一、选择题
-
1. 已知a,b是实数,则“a>|b|”是“a2>b2”的( )A、充分必要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件2. 函数f(x)=2x﹣ 的图象关于( )A、y轴对称 B、直线y=﹣x对称 C、直线y=x对称 D、坐标原点对称3. 某几何体的三视图如图所示,则它的体积是( )
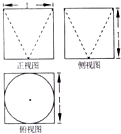 A、 B、 C、 D、4. 函数f(x)= (ω>0),|φ|< )的部分图象如图所示,则f(π)=( )
A、 B、 C、 D、4. 函数f(x)= (ω>0),|φ|< )的部分图象如图所示,则f(π)=( ) A、4 B、2 C、2 D、5. x、y满足约束条件 ,若z=y﹣ax取得最大值的最优解不唯一,则实数a的值为( )A、 或﹣1 B、2或 C、2或1 D、2或﹣16. 设向量 =(cosα,sinα), =(cosβ,sinβ),其中0<α<β<π,若|2 + |=| ﹣2 |,则β﹣α等于( )A、 B、﹣ C、 D、﹣7. 如图所示,A,B,C是双曲线 =1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是( )
A、4 B、2 C、2 D、5. x、y满足约束条件 ,若z=y﹣ax取得最大值的最优解不唯一,则实数a的值为( )A、 或﹣1 B、2或 C、2或1 D、2或﹣16. 设向量 =(cosα,sinα), =(cosβ,sinβ),其中0<α<β<π,若|2 + |=| ﹣2 |,则β﹣α等于( )A、 B、﹣ C、 D、﹣7. 如图所示,A,B,C是双曲线 =1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是( ) A、 B、 C、 D、38. 已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2 , 若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、38. 已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2 , 若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )A、 B、 C、 D、二、填空题
-
9. 集合A={0,|x|},B={1,0,﹣1},若A⊆B,则A∩B= , A∪B= , ∁BA= .10. 已知直线l1:ax+2y+6=0,l2:x+(a﹣1)y+a2﹣1=0,若l1⊥l2 , 则a= , 若l1∥l2 , 则l1与l2的距离为11. 若f(x)= ,则f(f(﹣1))= , f(f(x))≥1的解集为 .
12. 设数列{ }是公差为d的等差数列,若a3=2,a9=12,则d=;a12=13. 设抛物线y2=4x的焦点为F,P为抛物线上一点(在第一象限内),若以PF为直径的圆的圆心在直线x+y=2上,则此圆的半径为14. 设二次函数f(x)=ax2﹣4x+c(a≠0)的值域为[0,+∞),且f(1)≤4,则 的最大值是 .15. 各棱长都等于4的四面ABCD中,设G为BC的中点,E为△ACD内的动点(含边界),且GE∥平面ABD,若 • =1,则| |= .三、解答题
-
16. 设函数f(x)= • ,其中向量 =(2cosx,1), =(cosx, sin2x),x∈R.(1)、求f(x)的最小正周期与单调递减区间;(2)、在△ABC中,a、b、c分别是角A、B、C的对边,已知f(A)=2,b=1,△ABC的面积为 ,求 的值.17. 已知数列{an}的前n项和为Sn , 若a1=1,且Sn=tan﹣ ,其中n∈N*.(1)、求实数t的值和数列{an}的通项公式;(2)、若数列{bn}满足bn=log3a2n , 求数列{ }的前n项和Tn .18. 如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90℃,BC=2AD,△PAB与△PAD都是等边三角形,平面ABCD⊥平面PBD.
(I)证明:CD⊥平面PBD;
(II)求二面角A﹣PD﹣C的余弦值.

