2018-2019学年数学人教版八年级上册第11章 三角形 单元检测b卷
试卷更新日期：2018-08-13 类型：单元试卷
一、选择题
-
1. 以下列各组线段为边，能组成三角形的是（ ）A、2、2、4 B、8、6、3 C、2、6、3 D、11、4、62. 如图，△ABC中，∠A＝46°，∠C＝74°，BD平分∠ABC，交AC于点D，那么∠BDC的度数是（ ）
A、76° B、81° C、92° D、104°3. 下列实际情景运用了三角形稳定性的是（ ）A、人能直立在地面上 B、校门口的自动伸缩栅栏门 C、古建筑中的三角形屋架 D、三轮车能在地面上运动而不会倒4. 在四边形ABCD中，∠A＝∠B＝∠C，点E在边AB上，∠AED＝60°，则一定有（ ）A、∠ADE＝20° B、∠ADE＝30° C、∠ADE＝ ∠ADC D、∠ADE＝ ∠ADC5. 如图，已知BD是△ABC的中线，AB＝5，BC＝3，且△ABD的周长为11，则△BCD的周长是（ ）
A、9 B、14 C、16 D、不能确定6. 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（ ）A、108° B、90° C、72° D、60°7. 若a、b、c是△ABC的三边的长，则化简|a﹣b﹣c|﹣|b﹣c﹣a|+|a+b﹣c|=（ ）A、a+b+c B、﹣a+3b﹣c C、a+b﹣c D、2b﹣2c8. 如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点O，测得OA=15米，OB=10米，A、B间的距离不可能是（ ）
A、5米 B、10米 C、15米 D、20米9. 如图，已知点D是△ABC的重心，若AE＝4，则AC的长度为（ ）
A、4 B、8 C、10 D、1210. 如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点．若∠A＝60°，则∠BMN的度数为（ ）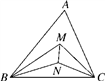
A、45° B、50° C、60° D、65°11. 小明同学在用计算器计算某n边形的内角和时，不小心多输入一个内角，得到和为2016°，则n等于（ ）
A、11 B、12 C、13 D、14二、填空题
-
12. 如图，共有个三角形．
13. 若n边形内角和为900°，则边数n= ．
14. 一个三角形的两边长分别是3和8，周长是偶数，那么第三边边长是.15. 如图，在△ABC中，CD是AB边上的中线，E是AC的中点，已知△DEC的面积是4cm2 ， 则△ABC的面积是.
16. 如图，把三角形纸片ABC沿DE折叠，使点A落在四边形BCDE的内部，已知∠1＋∠2＝80°，则∠A的度数为 .
17. 如图，已知∠AOB＝7°，一条光线从点A出发后射向OB边．若光线与OB边垂直，则光线沿原路返回到点A，此时∠A＝90°－7°＝83°.当∠A＜83°时，光线射到OB边上的点A1后，经OB反射到线段AO上的点A2 ， 易知∠1＝∠2.若A1A2⊥AO，光线又会沿A2→A1→A原路返回到点A，此时∠A＝76°.…若光线从A点出发后，经若干次反射能沿原路返回到点A，则锐角∠A的最小值为.
三、解答题
-
18. 如果多边形的每个内角都比它相邻的外角的4倍多30°，求这个多边形的内角和及对角线的总条数．
19. 如图，在△ABC中，AB＝AC，AC边上的中线BD把△ABC的周长分成12cm和15cm两部分，求△ABC各边的长．
20. 如图，点E在AC上，点F在AB上，BE，CF交于点O，且∠C＝2∠B，∠BFC－∠BEC＝20°，求∠C的度数．
21. 如图，在△BCD中，BC=4，BD=5．
(1)、求CD的取值范围；(2)、若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．22. 如图：
(1)、在△ABC中，BC边上的高是；
(2)、在△AEC中，AE边上的高是；
(3)、若AB＝CD＝2cm，AE＝3cm，求△AEC的面积及CE的长．
23. 如图，六边形ABCDEF的内角都相等，CF∥AB.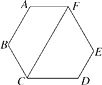
(1)、求∠FCD的度数；(2)、求证：AF∥CD.24. 如图，AD为△ABC的中线，BE为△ABD的中线．
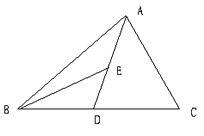(1)、∠ABE=15°，∠BAD=40°，求∠BED的度数；(2)、作图：在△BED中作出BD边上的高EF；BE边上的高DG；(3)、若△ABC的面积为40，BD=5，则△BDE 中BD边上的高EF为多少？若BE=6，求△BED中BE边上的高DG为多少？25. 如图①，在平面直角坐标系中，A(0，1)，B(4，1)，C为x轴正半轴上一点，且AC平分∠OAB.
(1)、求证：∠OAC＝∠OCA；(2)、如图②，若分别作∠AOC的三等分线及∠OCA的外角的三等分线交于点P，即满足∠POC＝ ∠AOC，∠PCE＝ ∠ACE，求∠P的大小；(3)、如图③，在(2)中，若射线OP、CP满足∠POC＝ ∠AOC，∠PCE＝ ∠ACE，猜想∠OPC的大小，并证明你的结论(用含n的式子表示)．