2018-2019学年数学人教版八年级上册第11章 三角形 单元检测a卷
试卷更新日期：2018-08-13 类型：单元试卷
一、选择题
-
1. 以下列各组线段为边，能组成三角形的是（ ）A、2cm，3cm，5cm B、5cm，6cm，10cm C、1cm，1cm，3cm D、3cm，4cm，9cm2. 任何一个三角形的三个内角中至少有（ ）A、一个角大于60° B、两个锐角 C、一个钝角 D、一个直角3. 一个三角形的两边长为2和6，第三边为偶数，则这个三角形的周长为（ ）A、10 B、12 C、14 D、164. 下列说法中正确的是（ ）A、三角形的角平分线和中线都是线段 B、三角形的角平分线和中线都是射线 C、三角形的角平分线是射线，而中线是线段 D、三角形的角平分线是线段，而中线是射线5. 如果多边形的内角和是外角和的k倍，那么这个多边形的边数是（ ）．A、k B、2k＋1 C、2k＋2 D、2k－26. 如果一个角的两边分别垂直于另一个角的两边，那么这两个角的数量关系为（ ）A、相等 B、互补 C、相等或互补 D、无法确定7. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（ ）
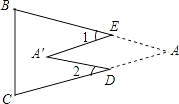A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2（∠1+∠2）8. 下列说法错误的是（ ）．A、锐角三角形的三条高线、三条中线、三条角平分线分别交于一点 B、钝角三角形有两条高线在三角形外部 C、直角三角形只有一条高线 D、任意三角形都有三条高线、三条中线、三条角平分线9. 四边形没有稳定性，当四边形形状改变时，发生变化的是（ ）．A、四边形的边长 B、四边形的周长 C、四边形的某些角的大小 D、四边形的内角和10. 如图，△ABC中，D，E分别是BC上两点，且BD=DE=EC，则图中面积相等的三角形有（ ）
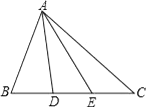A、4对 B、5对 C、6对 D、7对11. 如图所示，CD是△ABC的高，且CD＝5，S△ABC＝25，则AB的长（ ）
A、10 B、12 C、24 D、1812. 在下列条件中：①∠A+∠B=∠C，②∠A：∠B：∠C=1：2：3，③∠A=90°﹣∠B，④∠A=∠B=∠C中，能确定△ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图，电线杆上的横梁下方用三角形的支架支撑的理论根据是.
14. 如图，∠ABD与∠ACE是△ABC的两个外角，若∠A＝70°，则∠ABD＋∠ACE＝.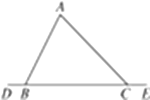
15. 已知：直线l1∥l2 ， 一块含30°角的直角三角板如图所示放置，∠1＝25°，则∠2等于.
16. 如果一个n边形的内角和是1440°，那么n= ．17. 如图所示，∠1+∠2+∠3+∠4+∠5+∠6=度．
18. 如果一个多边形的每一外角都是30°，则这个多边形对角线的条数是 ， 它的内角和是 ， 它的外角和是 ．
三、解答题
-
19. 在五边形ABCDE中，∠A=135°，AE⊥ED，AB∥CD，∠B=∠D，试求∠C的度数.
20. 一个正多边形的一个外角等于它的一个内角的 ，这个正多边形是几边形？21. 如图所示，直线AD和BC相交于O，AB∥CD，∠AOC=95°，∠B=50°，求∠A和∠D．
22. 如图，经测量，B处在A处的南偏西57°的方向，C处在A处的南偏东15°方向，C处在B处的北偏东82°方向，求∠C的度数．
23. 已知三角形三边长分别为a、b、c，其中a、b满足（a﹣6）2+|b﹣8|=0，求这个三角形最长边c的取值范围．24. 如图：
(1)、在△ABC中，BC边上的高是；(2)、在△AEC中，AE边上的高是；(3)、若AB＝CD＝2cm，AE＝3cm，求△AEC的面积及CE的长．
25. 如图
(1)、如图（1），在△ABC中，AD、AE分别是△ABC的高和角平分线，已知：∠B=30°，∠C=50°．求∠DAE的度数；(2)、如图（2），∠BAC的角平分线AF交BC于点E，过点F作FD⊥BC于点D，若∠B = x°，∠C =（x+30）°①∠CAE =（含x的代数式表示）②求∠F的度数．
26. 如图，在△ABC中，∠B＝∠C＝45°，点D在BC边上，点E在AC边上，且∠ADE＝∠AED，连接DE.
(1)、当∠BAD＝60°时，求∠CDE的度数；(2)、当点D在BC(点B、C除外)边上运动时，试写出∠BAD与∠CDE的数量关系，并说明理由．