2018-2019学年数学人教版八年级上册11.3.2 多边形 的内角和 同步训练
试卷更新日期：2018-08-13 类型：同步测试
一、选择题
-
1. 一个多边形的内角和是900°，这个多边形的边数是（ ）A、4 B、5 C、6 D、72. 四边形ABCD中，若∠A+∠C+∠D=280°，则∠B的度数为（ ）A、80° B、90° C、170° D、20°3. 七边形外角和为（ ）A、180° B、360° C、900° D、1 260°4. 一个六边形的内角和等于（ ）A、180° B、360° C、540° D、720°5. 一个正多边形的每个外角都是 ，这个正多边形是（ ）A、正六边形 B、正八边形 C、正十边形 D、正十二边形6. 不能作为正多边形的内角的度数的是（ ）A、120° B、108° C、144° D、145°7. 四边形的四个内角（ ）A、可以都是锐角 B、可以都是钝角 C、可以都是直角 D、必须有两个锐角8. 多边形的每个内角都等于150°，则从此多边形的一个顶点出发可作的对角线共有（ ）A、8条 B、9条 C、10条 D、11条
二、填空题
-
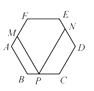
9. 若一个多边形每个外角都等于它相邻的内角的 ，则这个多边形的边数为.10. 在四边形ABCD中，若∠A∶∠B∶∠C∶∠D=3∶1∶2∶3，则该四边形中最大的角的度数是.11. 一个多边形的边数每增加1条，其内角和就增加 ， 其外角和.12. 如图，正六边形ABCDEF，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N.则∠MPN=.
13. 如图，小兰在操场上散步。她从O点出发，面向正东方向走5m，然后向左转45°，再向前走5m，又向左转45°，再向前走5m.这样一直走下去，第一次回到出发点O时，她共走了m
14. 如图，在四边形ABCD中，∠α，∠β分别是∠BAD、∠BCD相邻的补角，且∠B＋∠CDA＝140°，则∠α＋∠β等于 ．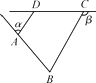
三、解答题
-
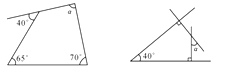
15. 一个多边形的外角和是内角和的 ，求这个多边形的边数．16. 求下图中∠α的度数.
17. 如图所示模板，按规定AB，CD的延长线相交成80°的角，因交点不在板上不便测量，工人师傅测得∠BAE＝122°，∠DCF＝155°，此时AB，CD的延长线相交所成的角是否符合规定？为什么？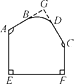
18. 一个多边形的内角和与某一个外角的度数总和为1350°，求这个多边形的边数．19. 四边形ABCD中，∠A=140°，∠D=80°.
(1)、如图1，若∠B=∠C，试求出∠C的度数；(2)、如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数.20.
(1)、如图①②，试研究其中∠1、∠2与∠3、∠4之间的数量关系；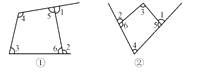
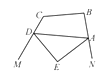
(2)、如果我们把∠1、∠2称为四边形的外角，那么请你用文字描述上述的关系式；(3)、用你发现的结论解决下列问题：如图，AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线，∠B+∠C=240°，求∠E的度数.
21. 如图1，线段AB、CD相交于点O，连结AD、CB，我们把这个图形称为“8字型”根据三角形内角和容易得到：∠A+∠D=∠C+∠B.
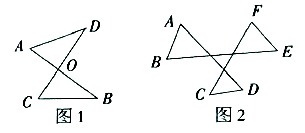
(1)、用“8字型”如图2，∠A+∠B+∠C+∠D+∠E+∠F=；
(2)、造“8字型”如图3，∠A+∠B+∠C+∠D+∠E+∠F+∠G=；
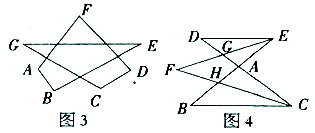
(3)、发现“8字型”如图4，BE、CD相交于点A，CF为∠BCD的平分
线，EF为∠BED的平分线.
①图中共有个“8字型”；
②若∠B：∠D：∠F=4：6：x，求x的值.22. 探究与发现：
图1 图2 图3
(1)、探究一：三角形的一个内角与另两个内角的平分线所夹的角之间的关系已知：如图1，在△ADC中，DP、CP分别平分∠ADC和∠ACD，
试探究∠P与∠A的数量关系，并说明理由．
(2)、探究二：四边形的两个个内角与另两个内角的平分线所夹的角之间的关系已知：如图2，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，
试探究∠P与∠A＋∠B的数量关系，并说明理由．
(3)、探究三：六边形的四个内角与另两个内角的平分线所夹的角之间的关系已知：如图3，在六边形ABCDEF中，DP、CP分别平分∠EDC和∠BCD，请直接写出∠P与∠A＋∠B＋∠E＋∠F的数量关系：