2018-2019学年数学人教版八年级上册11.2.1 三角形内角 同步训练
试卷更新日期：2018-08-13 类型：同步测试
一、选择题
-
1. 已知在△ABC中，∠A与∠C的度数比是5：7，且∠B比∠A大10°，那么∠B为（ ）A、40° B、50° C、60° D、70°2. 如图，∠A +∠B +∠C +∠D +∠E +∠F等于（ ）
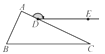
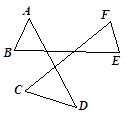A、180° B、360° C、540° D、720°3. 如图，已知AB⊥BD、AC⊥CD，∠CAD=35°，则∠ADC=（ ）
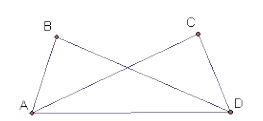A、35° B、65° C、55° D、45°4. 如图，在△ABC中，已知∠ABC=70°，∠ACB=60°，BE⊥AC于E，CF⊥AB于F，H是BE和CF的交点，则∠EHF=（ ）
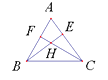A、100° B、110° C、120° D、130°5. 在△ABC中，已知∠A=4∠B=104°，则∠C的度数是（ ）A、50° B、45° C、40° D、30°6. 一个三角形三个内角的度数之比为1：2：3，则这个三角形一定是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形7. 如图，已知D、E在△ABC的边上，DE∥BC，∠B=60°，∠AED=45°，则∠A的度数为（ ）
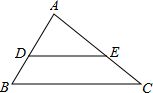A、65° B、75° C、85° D、95°8. 如图所示，AB∥CD，AD、BC相交于O，若∠A=∠COD=66°，则∠C为（ ）
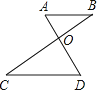A、66° B、38° C、48° D、58°9. 如图，在△ABC中，∠A=20°，∠ABC与∠ACB的角平分线交于D1 ， ∠ABD1与∠ACD1的角平分线交于点D2 ， 依此类推，∠ABD4与∠ACD4的角平分线交于点D5 ， 则∠BD5C的度数是（ ）
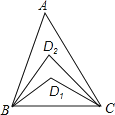A、24° B、25° C、30° D、36°二、填空题
-
10. 如图，△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠ADE=155°，则∠B的度数为.
11. 三角形中最大的内角不能小于度，最小的内角不能大于度．12. △ABC中，∠A=50°，∠B=60°，则∠C= ．13. 如图，∠1+∠2+∠3+∠4=度.
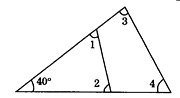14. 如图，在△ABC中，∠B=66°，∠C=54°，AD是∠BAC的平分线，DE平分∠ADC交AC于E，则∠ADE= ．
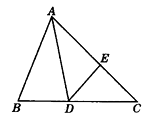15. 当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为 ．三、解答题
-
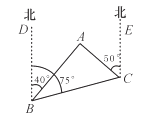
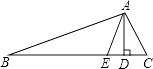
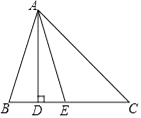
16. 在△ABC中，已知∠A= ∠B= ∠C，求∠A、∠B、∠C的度数．17. 如图，在△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，∠C=45°，求∠DAE与∠AEC的度数．
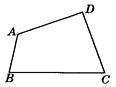
18. 如图是一个大型模板，设计要求BA与CD相交成30°角，DA与CB相交成20°角，怎样通过测量∠A，∠B，∠C，∠D的度数，来检验模板是否合格？
