2016-2017学年天津市红桥区高三上学期期中数学试卷(理科)
试卷更新日期:2017-02-21 类型:期中考试
一、选择题
-
1. 已知集合A={0,1,2,3,4,5},B={1,3,6,9},C={3,7,8},则(A∩B)∪C=( )A、{3} B、{3,7,8} C、{1,3,7,8} D、{1,3,6,7,8}2. 把函数y=sinx(x∈R)的图象上所有的点向左平行移动 个单位长度,再把所得图象上所有点的横坐标缩短到原来的 (纵坐标不变),得到的图象所表示的函数是( )A、 ,x∈R B、 ,x∈R C、 ,x∈R D、 ,x∈R3. 函数f(x)=2sin(ωx+φ)(ω>0,﹣ <φ< )的部分图象如图所示,则ω,φ的值分别是( )
 A、2,﹣ B、2,﹣ C、4,﹣ D、4,4. 设a=20.3 , b=0.32 , c=log20.3,则a,b,c的大小关系是( )A、a<b<c B、c<b<a C、c<a<b D、b<c<a5. ;给定函数① ,② ,③y=|x﹣1|,④y=2x+1 , 其中在区间(0,1)上单调递减的函数序号是( )A、①② B、②③ C、③④ D、①④6. 函数f(x)=ln(x+1)﹣ 的零点所在的大致区间是( )A、(0,1) B、(1,2) C、(2,e) D、(3,4)7. 函数y= 的图象大致是( )A、
A、2,﹣ B、2,﹣ C、4,﹣ D、4,4. 设a=20.3 , b=0.32 , c=log20.3,则a,b,c的大小关系是( )A、a<b<c B、c<b<a C、c<a<b D、b<c<a5. ;给定函数① ,② ,③y=|x﹣1|,④y=2x+1 , 其中在区间(0,1)上单调递减的函数序号是( )A、①② B、②③ C、③④ D、①④6. 函数f(x)=ln(x+1)﹣ 的零点所在的大致区间是( )A、(0,1) B、(1,2) C、(2,e) D、(3,4)7. 函数y= 的图象大致是( )A、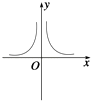 B、
B、 C、
C、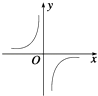 D、
D、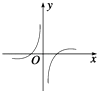 8. 如图所示,由抛物线y2=x和直线x=1所围成的图形的面积等于( )
8. 如图所示,由抛物线y2=x和直线x=1所围成的图形的面积等于( ) A、1 B、 C、 D、9. 以下说法正确的有( )
A、1 B、 C、 D、9. 以下说法正确的有( )(1)y=x+ (x∈R)最小值为2;
(2)a2+b2≥2ab对a,b∈R恒成立;
(3)a>b>0且c>d>0,则必有ac>bd;
(4)命题“∃x∈R,使得x2+x+1≥0”的否定是“∀x∈R,使得x2+x+1≥0”;
(5)实数x>y是 < 成立的充要条件;
(6)设p,q为简单命题,若“p∨q”为假命题,则“¬p∨¬q”也为假命题.
A、2个 B、3个 C、4个 D、5个10.已知函数f(x)的定义域为[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
x
﹣1
0
4
5
f(x)
1
2
2
1
(1)函数y=f(x)是周期函数;
(2)函数f(x)在(0,2)上是减函数;
(3)如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
(4)当1<a<2时,函数y=f(x)﹣a有4个零点.
其中真命题的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. |2x﹣1|≥3的解集是 .12. 已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积为 .13. 如果函数f(x)=ax2+2x﹣3在区间(﹣∞,4)上是单调递增的,则实数a的取值范围是 .14. 已知函数f(x)= 那么不等式f(x)≥1的解集为 .15. 若f(x)= ,则 f(x)dx= .16. 已知函数y=f(x)的导函数y=f'(x)的图象如图所示,给出如下命题:
①0是函数y=f(x)的一个极值点;
②函数y=f(x)在 处切线的斜率小于零;
③f(﹣1)<f(0);
④当﹣2<x<0时,f(x)>0.
其中正确的命题是 . (写出所有正确命题的序号)

三、解答题
-
17. 已知一元二次不等式x2﹣ax﹣b<0的解集是{x|1<x<3}.(1)、求实数a,b的值;(2)、解不等式 >1.18. 设命题p:关于m的不等式:m2﹣4am+3a2<0,其中a<0,命题q:∀x>0,使x+ ≥1﹣m恒成立,且p是q的充分不必要条件,求a的取值范围.19. 设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅰ)求B的大小;
(Ⅱ)若 ,c=5,求b.
20. 已知函数f(x)= (sin2x﹣cos2x)+2sinxcosx.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)设x∈[﹣ , ],求f(x)的值域和单调递增区间.
21. 已知函数f(x)=x3﹣ax﹣1.(1)、若f(x)在(﹣∞,+∞)上单调递增,求实数a的取值范围;(2)、是否存在实数a,使f(x)在(﹣1,1)上单调递减?若存在,求出a的取值范围;若不存在试说明理由.22. 已知函数f(x)=lnx﹣a(x﹣1),其中a>0.(Ⅰ)若函数f(x)在(0,+∞)上有极大值0,求a的值;(提示:当且仅当x=1时,lnx=x﹣1);
(Ⅱ)令F(x)=f(x)+a(x﹣1)+ (0<x≤3),其图象上任意一点P(x0 , y0)处切线的斜率k≤ 恒成立,求实数a的取值范围;
(Ⅲ)讨论并求出函数f(x)在区间 上的最大值.