2015-2016学年江西省赣州市石城县七年级下学期期中数学试卷

试卷更新日期：2017-02-21 类型：期中考试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，点P（﹣3，4）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 观察下列选项中的图案，能通过图案（1）平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 过点P向线段AB所在直线画垂线，画图正确的是（）

A、 B、 C、 D、

查看试题解析
4. 在实数：3.14159， $\sqrt[3]{64}$ ，1.010010001…， $4. \dot{2} \dot{1}$ ，π， $\frac{22}{7}$ 中，无理数的（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列各式中，正确的是（）

A、 $\sqrt{16}$ =±4 B、± $\sqrt{16}$ =4 C、 $\sqrt[3]{- 27}$ =﹣3 D、 $\sqrt{{(- 4)}^{2}}$ =﹣4

查看试题解析
6. 下列命题是真命题的是（）

A、如果两个角不相等，那么这两个角不是对顶角 B、两个互补的角一定是邻补角 C、如果两个角是同位角，那么这两个角一定相等 D、如果a²=b² ，那么a=b

查看试题解析
7. 在平面直角坐标系中，已知线段AB的两个端点分别是A（﹣4，﹣1），B（1，1），将线段AB平移后得到线段A′B′，若点A′的坐标为（﹣2，2），则点B′的坐标为（）

A、（4，3） B、（3，4） C、（﹣1，﹣2） D、（﹣2，﹣1）

查看试题解析
8. 为新建一个以环保为主题的公园，某地开辟了一块长方形的荒地，已知这块荒地的长是宽的3倍，它的面积为120000m² ，那么公园的宽为（）

A、200m B、400m C、600m D、200m或600m

查看试题解析
9. 如图，OE是∠AOB的平分线，CD∥OB交OE于点D，∠ACD=50°，则∠CDE的度数为（）

A、125° B、130° C、140° D、155°

查看试题解析
10. 若将一副三角板按如图所示的方式放置，则下列结论不正确的是（）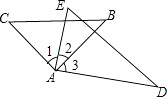

A、∠1=∠3 B、如果∠2=30°，则有AC∥DE C、如果∠2=30°，则有BC∥AD D、如果∠2=30°，必有∠4=∠C

查看试题解析

二、填空题

11. 49的算术平方根是．

查看试题解析
12. 已知直线a∥b，b∥c，则直线a、c的位置关系是．

查看试题解析
13. 点C在x轴的下方，y轴的右侧，距离x轴3个单位长度，距离y轴5个单位长度，则点C的坐标为．

查看试题解析
14. 实数a、b在数轴上的位置如图所示，则化简|a+b|+|b﹣a|=

查看试题解析
15. 如图1所示的是一个长方形纸带，∠DEF=25°，将纸带沿EF折叠成图2，则图2中的∠BGE的度数是．

查看试题解析
16. 在平面直角坐标系中，已知点A₁（1，1），A₂（2，4），A₃（3，9），A₄（4，16），…，用你发现的规律确定点A₂₀₁₆的坐标为

查看试题解析

三、解答题

17. 解方程与化简

(1)、求等式中x的值：4x²﹣9=0

(2)、化简求值： $\sqrt{0.09}$ ﹣ $\sqrt[3]{- 8}$ ．

查看试题解析
18. 某市有A、B、C、D四个大型超市，分别位于一条东西走向的平安大路两侧，如图，若C（﹣2，8）、D（0，0），请建立适当的直角坐标系，并写出A、B两个超市相应的坐标．

查看试题解析
19. 如图，在平面直角坐标系中，三角形ABC的三个顶点的坐标分别为A（﹣2，5）、B（﹣4，3）、C（﹣1，1），请作出三角形ABC向右平移5个单位后得到的三角形A₁B₁C₁ ，并求出三角形ABC的面积．

查看试题解析
20. 已知一个正方体的体积是1000cm³ ，现在要在它的8个角上分别截去8个大小相同的小正方体，使截去后余下的体积是488cm³ ，问截得的每个小正方体的棱长是多少？

查看试题解析
21. 已知，如图，AD⊥BC，EF⊥BC，∠BEF=∠ADG．
求证：DG∥AB．把证明的过程填写完整．
证明：因为AD⊥BC，EF⊥BC（已知），
所以∠EFB=∠ADB=90°（）
所以EF∥（）
所以∠BEF=（）
因为∠BEF=∠ADG（已知）
所以（）
所以DG∥AB（）

查看试题解析
22. 如图，AB和CD相交于点O，∠DOE=90°，若∠BOE= $\frac{1}{2}$ ∠AOC．

(1)、指出与∠BOD相等的角，并说明理由；

(2)、求∠BOD，∠AOD的度数．

查看试题解析
23. 已知点A（a，0）、B（b，0），且（a+4）²+|b﹣2|=0．

(1)、求a、b的值．

(2)、在y轴的正半轴上找一点C，使得三角形ABC的面积是15，求出点C的坐标．

(3)、过（2）中的点C作直线MN∥x轴，在直线MN上是否存在点D，使得三角形ACD的面积是三角形ABC面积的 $\frac{1}{2}$ ？若存在，求出点D的坐标；若不存在，请说明理由．

查看试题解析
24. 如图1，已知直线l₁∥l₂ ，且l₁、l₂分别相交于A、B两点，l₄和l₁、l₂分别交于C、D两点，∠ACP=∠1，∠BDP=∠2，∠CPD=∠3．点P在线段AB上．

(1)、若∠1=22°，∠2=33°，则∠3= ．

(2)、试找出∠1、∠2、∠3之间的等量关系，并说明理由．

(3)、应用（2）中的结论解答下列问题：
如图2，点A在B处北偏东40°的方向上，在C处的北偏西45°的方向上，求∠BAC的度数．

(4)、如果点P在直线l₃上且在A、B两点外侧运动时，其他条件不变，试探究∠1、∠2、∠3之间的关系（点P和A、B两点不重合），直接写出结论即可．

查看试题解析