2015-2016学年江苏省无锡市宜兴市丁蜀学区七年级下学期期中数学试卷

试卷更新日期：2017-02-21 类型：期中考试

进入出卷网下载

一、选择题．

1. 下列计算正确的是（）

A、（a²）³=a⁵ B、a⁶÷a³=a³ C、aⁿ•aⁿ=2aⁿ D、a²+a²=a⁴

查看试题解析
2. 下列由左到右的变形中属于因式分解的是（）

A、24x²y=3x•8xy B、m²﹣2m﹣3=m（m﹣2）﹣3 C、x²+2x+1=（x+1）² D、（x+3）（x﹣3）=x²﹣9

查看试题解析
3. 一个多边形的每个内角都等于144°，则这个多边形的边数是（）

A、8 B、9 C、10 D、11

查看试题解析
4. ∠1与∠2是直线a、b被直线c所截得的同位角，∠1与∠2的大小关系是（）

A、∠1=∠2 B、∠1＞∠2 C、∠1＜∠2 D、无法确定

查看试题解析
5. 若a=﹣0.3² ， b=﹣3^﹣² ， c= ${(- \frac{1}{2})}^{- 2}$ ，d=（﹣ $\frac{1}{3}$ ）⁰ ，则它们的大小关系是（）

A、a＜b＜c＜d B、b＜a＜d＜c C、a＜d＜c＜b D、c＜a＜d＜b

查看试题解析
6. 如图，在边长为2a的正方形中央剪去一边长为（a+2）的小正方形（a＞2），将剩余部分剪开密铺成一个平行四边形，则该平行四边形的面积为（）

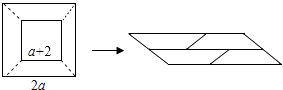A、a²+4 B、2a²+4a C、3a²﹣4a﹣4 D、4a²﹣a﹣2

查看试题解析
7. 如图，直线AB∥CD，直线EF分别交直线AB，CD于点E，F，过点F作FG⊥FE，交直线AB于点G，若∠1=42°，则∠2的大小是（）

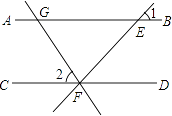A、56° B、48° C、46° D、40°

查看试题解析
8. 如图，∠B+∠C+∠D+∠E﹣∠A等于（）

A、360° B、300° C、180° D、240°

查看试题解析
9. 不论x、y为何有理数，多项式x²+y²﹣4x﹣2y+8的值总是（）

A、正数 B、零 C、负数 D、非负数

查看试题解析
10. 如图，在△ABC中，E，F分别是AD，CE边的中点，且S_△_BEF=4cm² ，则S_△_ABC为（）

A、1cm² B、2cm² C、8cm² D、16cm²

查看试题解析

二、填空题．

11. b^m•b³^﹣^m=
（﹣a^m）³= ．

查看试题解析
12. 世界上最小的开花结果植物是澳大利亚的出水浮萍，其果实的质量只有0.000 00076克．用科学记数法表示这个质量是克．

查看试题解析
13. 若x²﹣ax+16是一个完全平方式，则a=

查看试题解析
14. 若（x﹣2）⁰=1，则满足条件的x的取值范围是．

查看试题解析
15. 一个三角形的两边长分别是1和4，那么第三边x的取值范围

查看试题解析
16. 已知2m+5n﹣3=0，则4^m×32ⁿ的值为．

查看试题解析
17. 若（x²+px+8）•（x²﹣3x+1）的结果中不含x³项，则P=

查看试题解析
18. 要在台阶上铺设某种红地毯，已知这种红地毯每平方米的售价是40元，台阶宽为3米，侧面如图所示．购买这种红地毯至少需要元．

查看试题解析
19.
将边长为1的正方形纸片按图1所示方法进行对折，记第1次对折后得到的图形面积为S₁ ，第2次对折后得到的图形面积为S₂ ， …，第n次对折后得到的图形面积为S_n ，请根据图2化简，S₁+S₂+S₃+…+S₂₀₁₄=

查看试题解析

三、解答题

20. 计算：

(1)、（﹣1）² $+ {(\frac{1}{5})}^{0} + {(\frac{1}{5})}^{- 2}$

(2)、[（﹣3a）²+3ab²c]•2ab²

(3)、（﹣ $\frac{1}{3}$ ）¹⁰⁰×3¹⁰¹

(4)、（2a+b）（b﹣2a）﹣（a﹣3b）² ．

查看试题解析
21. 分解因式：

(1)、x²﹣y²

(2)、b²+6b+9

(3)、x⁴﹣9x²

(4)、﹣3x³+6x²y﹣3xy²

(5)、2x（a﹣b）﹣（b﹣a）

(6)、m³﹣m²﹣20m．

查看试题解析
22. 先化简，再求值：（3x+2）（3x﹣2）﹣5x（x+1）﹣（x﹣1）² ，其中x²﹣x﹣ $\frac{2}{3} = 0$ ．

查看试题解析
23. 已知a^m=2，aⁿ=4，求①a^m⁺ⁿ的值；②a^4m^﹣²ⁿ的值．

查看试题解析
24. 已知a﹣b=3，ab=2，求下列各式的值．

(1)、a²+b²

(2)、（a+b）² ．

查看试题解析
25. 如图，已知∠ABC+∠ECB=180°，∠P=∠Q，

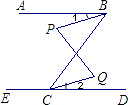(1)、AB与ED平行吗？为什么？

(2)、∠1与∠2是否相等？说说你的理由．

查看试题解析
26. 一天，小明和小玲玩纸片拼图游戏，发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．比如图②可以解释为：（a+2b）（a+b）=a²+3ab+2b² ．

(1)、图③可以解释为等式：

(2)、要拼出一个长为a+3b，宽为2a+b的长方形，需要如图所示的块，块，块．

(3)、如图④，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个矩形的两边长（x＞y），观察图案，指出以下关系式：（1） $x y = \frac{m^{2} - n^{2}}{4}$ （2）x+y=m（3）x²﹣y²=m•n（4） $x^{2} + y^{2} = \frac{m^{2} + n^{2}}{2}$
其中正确的有

A、1个 B、2个 C、3个 D、4个．

查看试题解析
27. Rt△ABC中，∠C=90°，点D，E分别是边AC，BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．

(1)、若点P在线段AB上，如图①，且∠α=50°，则∠1+∠2=；

(2)、若点P在斜边AB上运动，如图②，则∠α、∠1、∠2之间的关系为；

(3)、如图③，若点P在斜边BA的延长线上运动（CE＜CD），请直接写出∠α、∠1、∠2之间的关系：；

(4)、若点P运动到△ABC形外（只需研究图④情形），则∠α、∠1、∠2之间有何关系？并说明理由．

查看试题解析