2015-2016学年河南省南阳市唐河县七年级下学期期中数学试卷

试卷更新日期：2017-02-21 类型：期中考试

进入出卷网下载

一、选择题

1. 下列方程中，解是x=2的是（）

A、3x+1=2x﹣1 B、3x﹣1=2x+1 C、3x+2x﹣2=0 D、3x+2x+2=0

查看试题解析
2. 如图所示的两架天平保持平衡，且每块巧克力的质量相等，每个果冻的质量也相等，则一块巧克力的质量是（）

A、10g B、15g C、30 D、20g

查看试题解析
3. a，b都是实数，且a＜b，则下列不等式的变形正确的是（）

A、a+x＞b+x B、﹣a+1＜﹣b+1 C、3a＜3b D、 $\frac{a}{2}$ ＞ $\frac{b}{2}$

查看试题解析
4. 不等式组 ${\begin{matrix} 2 x + 2 > 0 \\ - x \geq - 1 \end{matrix}$ 的解在数轴上表示为（）

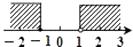A、 B、 C、 D、

查看试题解析
5. 以长为8cm、6cm、10cm、4cm的四条线段中的三条线段为边，可以画出三角形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} m x + n y = 8 \\ n x - m y = 1 \end{matrix}$ 的解，则2m﹣n的值是（）

A、4 B、2 C、 $\sqrt{2}$ D、﹣4

查看试题解析
7. 下列说法中错误的是（）

A、三角形的中线、角平分线、高线都是线段 B、任意三角形的内角和都是180° C、三角形按边分可分为不等边三角形和等腰三角形 D、三角形的一个外角大于任何一个内角

查看试题解析
8. 下列四组数值中，为方程组 ${\begin{matrix} x + 2 y + z = 0 \\ 2 x - y - z = 1 \\ 3 x - y - x = 2 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 0 \\ y = 1 \\ z = - 2 \end{matrix}$ B、 ${\begin{matrix} x = 1 \\ y = 0 \\ z = 1 \end{matrix}$ C、 ${\begin{matrix} x = 0 \\ y = - 1 \\ z = 0 \end{matrix}$ D、 ${\begin{matrix} x = 1 \\ y = - 2 \\ z = 3 \end{matrix}$

查看试题解析

二、填空题

9. 在方程①x﹣2= $\frac{3}{x}$ ，②0.3y=1，③x²﹣5x+6=0，④x=0，⑤6x﹣y=9，⑥ $\frac{2 x + 1}{3} = \frac{1}{6} x$ 中，是一元一次方程的有．

查看试题解析
10. 某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打折．

查看试题解析
11. 不等式3x﹣2≤5x+6的所有负整数解的和为

查看试题解析
12. 已知不等式组 ${\begin{matrix} x + 2 > m + n \\ x - 1 < m - 1 \end{matrix}$ 的解集为﹣1＜x＜2，则（m+n）²⁰¹⁷= ．

查看试题解析
13. 轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/小时，水速为2千米/时，则A港和B港相距千米．

查看试题解析
14. 已知关于x，y的方程组 ${\begin{matrix} x + y = 5 \\ 4 a x + 5 b y = - 22 \end{matrix}$ 与 ${\begin{matrix} 2 x - y = 1 \\ a x - b y - 8 = 0 \end{matrix}$ 有相同的解，则（3a+2b）²⁰¹⁷的值为．

查看试题解析
15. 已知关于x的方程ax+b=0，有以下四种说法：
①若x=1是该方程的解，则a+b=0；②若a=﹣1，则x=b是该方程的解；
③若a≠0，则该方程的解是x=﹣ $\frac{b}{a}$ ；④若a=0，b≠0，则该方程无解．
其中所有正确说法的序号是．

查看试题解析

三、解答题

16. 解方程（组）：

(1)、 $\frac{x + 1}{2} = \frac{2 - x}{3} - 1$

(2)、解二元一次方程组 ${\begin{matrix} x - y = 8 ① \\ 3 x + y = 12 ② \end{matrix}$
有位同学是这么做的，①+②得4x=20，解得x=5，代入①得y=﹣3．
∴这个方程组的解为 ${\begin{matrix} x = 5 \\ y = - 3 \end{matrix}$ ．
该同学解这个二元一次方程组的过程中使用了消元法，目的是把二元一次方程组转化为求解；

(3)、请你换一种方法来求解（2）中二元一次方程组．

查看试题解析
17. 解不等式组． ${\begin{matrix} 2 x + 5 \leq 3 (x + 2) \\ 2 x - \frac{1 + 3 x}{2} < 1 \end{matrix}$ 把不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解．

查看试题解析
18. 如图，△ABC中，D、E分别是BC、AB边上的点，AD平分∠EDC，试说明∠BED＞∠B的道理．

查看试题解析
19. 试确定实数a的取值范围，使不等式组 ${\begin{matrix} \frac{x}{2} + \frac{x + 1}{3} > 0 \\ x + \frac{5 a + 4}{3} > \frac{4}{3} (x + 1) a \end{matrix}$ 恰有两个整数解．

查看试题解析
20. 学校计划购买40支钢笔，若干本笔记本（笔记本数超过钢笔数）．甲、乙两家文具店的标价都是钢笔10元/支，笔记本2元/本，甲店的优惠方式是钢笔打9折，笔记本打8折；乙店的优惠方式是每买5支钢笔送1本笔记本，钢笔不打折，购买的笔记本打7.5折，试问购买笔记本数在什么范围内到甲店更合算．

查看试题解析
21. 【提出问题】已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围．
【分析问题】先根据已知条件用一个量如y取表示另一个量如x，然后根据题中已知量x的取值范围，构建另一量y的不等式，从而确定该量y的取值范围，同法再确定另一未知量x的取值范围，最后利用不等式性质即可获解．
【解决问题】解：∵x﹣y=2，∴x=y+2．
又∵x＞1，∴y+2＞1，∴y＞﹣1．
又∵y＜0，∴﹣1＜y＜0，…①
同理得1＜x＜2…②
由①+②得﹣1+1＜y+x＜0+2．
∴x+y的取值范围是0＜x+y＜2．
【尝试应用】已知x﹣y=﹣3，且x＜﹣1，y＞1，求x+y的取值范围．

查看试题解析
22. 学校6名教师和234名学生集体外出活动，准备租用45座大车或30座小车．若租用1辆大车2辆小车共需租车费1000元；若租用2辆大车一辆小车共需租车费1100元．

(1)、求大、小车每辆的租车费各是多少元？

(2)、若每辆车上至少要有一名教师，且总租车费用不超过2300元，求最省钱的租车方案．

查看试题解析
23. 某文具商店销售功能相同的A、B两种品牌的计算器，购买2个A品牌和3个B品牌的计算器共需156元；购买3个A品牌和1个B品牌的计算器共需122元．

(1)、求这两种品牌计算器的单价；

(2)、学校开学前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A品牌计算器按原价的八折销售，B品牌计算器5个以上超出部分按原价的七折销售，设购买x个A品牌的计算器需要y₁元，购买x个B品牌的计算器需要y₂元，分别求出y₁、y₂关于x的函数关系式；

(3)、小明准备联系一部分同学集体购买同一品牌的计算器，若购买计算器的数量超过5个，购买哪种品牌的计算器更合算？请说明理由．

查看试题解析