浙江省温岭市2018届九年级数学中考一模试卷
试卷更新日期:2018-08-10 类型:中考模拟
一、单选题
-
1. 在 0.5, 0 , -1, -2 这四个数中,绝对值最大的数是( )
A、0.5 B、0 C、-1 D、-22. “厉行节约,反对浪费”势在必行.最新统计数据显示,我国每年浪费食物总量折合粮食大约是 210000000人一年的口粮,将 210000000 用科学记数法表示为( )A、2.1×109 B、0.21×109 C、2.1×108 D、21×1073. 不等式2x<10的解集在数轴上表示正确的是( )A、 B、
B、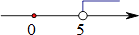 C、
C、 D、
D、 4.
4.如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( )
 A、
A、 B、
B、 C、
C、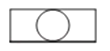 D、
D、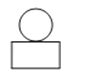 5. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、对角线互相垂直的四边形是菱形 C、菱形的对角线互相垂直 D、对角线互相平分的四边形是平行四边形6. 某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分,全班40名同学参加了此次竞赛,他们的得分情况如下表所示:
5. 下列说法中,错误的是( )A、平行四边形的对角线互相平分 B、对角线互相垂直的四边形是菱形 C、菱形的对角线互相垂直 D、对角线互相平分的四边形是平行四边形6. 某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分,全班40名同学参加了此次竞赛,他们的得分情况如下表所示:成绩(分)
50
60
70
80
90
100
人数
2
5
13
10
7
3
则全班40名同学的成绩的中位数和众数分别是( )
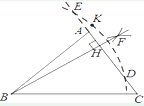
A、75,70 B、70,70 C、80,80 D、75,807. 小明用尺规作图作△ABC边AC上的高BH,作法如下:①分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.其中顺序正确的作图步骤是( )
 A、①②③④ B、④③②① C、②④③① D、④③①②8. 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A、①②③④ B、④③②① C、②④③① D、④③①②8. 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( ) A、点C B、点D或点E C、线段DE(异于端点) 上一点 D、线段CD(异于端点) 上一点9. 对于代数式 ax+b(a,b 是常数),当 x 分别等于 3、2、1、0 时,小虎同学依次求得下面四个结果:3、2、−1、−3,其中只有一个是错误的,则错误的结果是( )
A、点C B、点D或点E C、线段DE(异于端点) 上一点 D、线段CD(异于端点) 上一点9. 对于代数式 ax+b(a,b 是常数),当 x 分别等于 3、2、1、0 时,小虎同学依次求得下面四个结果:3、2、−1、−3,其中只有一个是错误的,则错误的结果是( )
A、3 B、2 C、−1 D、−310. 在平面直角坐标系中,如果 x 与 y 都是整数,就称点(x,y)为整点.下列命题中错误的是( )
A、存在这样的直线,既不与坐标轴平行,又不经过任何整点 B、若 k 与 b 都是无理数,则直线 y=kx+b 不经过任何整点 C、若直线 y=kx+b 经过无数多个整点,则 k 与 b 都是有理数 D、存在恰好经过一个整点的直线二、填空题
-
11. 9的算术平方根是 .12. 掷一枚质地均匀的正方体骰子(六个面上分别刻有1到6的点数),向上一面出现的点数大于2且小于5的概率为 .13. 一个物体重 100N,物体对地面的压强 P(单位:Pa)随物体与地面的接触面积 S(单位:㎡)变化而变化的函数关系式是.
14. 已知命题“对于非零实数 a,关于 x 的一元二次方程 ax2+4x- 1=0 必有实数根”,能说明这个命题是假命题的一个反例是.
15. 如图,在圆 O 中有折线 ABCO,BC=6,CO=4,∠B=∠C=60°,则弦 AB 的长为. 16. 对于一个函数,如果它的自变量 x 与函数值 y 满足:当−1≤x≤1 时,−1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=−x 均是“闭函数”. 已知 y = ax2+ bx + c(a≠0) 是“闭函数”,且抛物线经过点 A(1,−1)和点 B(−1,1),则 a 的取值范围是.
16. 对于一个函数,如果它的自变量 x 与函数值 y 满足:当−1≤x≤1 时,−1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=−x 均是“闭函数”. 已知 y = ax2+ bx + c(a≠0) 是“闭函数”,且抛物线经过点 A(1,−1)和点 B(−1,1),则 a 的取值范围是.三、解答题
-
17. 计算:
18. 某学生化简分式 出现了错误,解答过程如下:原式= (第一步)
= (第二步)
= .(第三步)
(1)、该学生解答过程是从第步开始出错的,其错误原因是;
(2)、请写出此题正确的解答过程.19. 小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角∠ABC =45°,为节省家里空间小明 想把垃圾桶放到桌下,经测量桌子下沿离地面高 55cm,垃圾桶高 BD=33.1cm,桶盖直径 BC=28.2cm,问垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(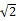 » 1.41 )
» 1.41 )
 20. 有这样一个问题:探究函数 的图象与性质,小静根据学习函数的经验,对函数 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
20. 有这样一个问题:探究函数 的图象与性质,小静根据学习函数的经验,对函数 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
(1)、函数 的自变量 x 的取值范围是;(2)、下表是 y 与 x 的几组对应值.
表中的 m=;
(3)、如图,在平面直角坐标系中,描出以上表中各对对应值为坐标 的点,根据描出的点画出该函数的图象; (4)、结合函数图象,写出一条该函数图象的性质:.
(4)、结合函数图象,写出一条该函数图象的性质:.
21. 如图,正方形 ABCD 的边长为 4,E 是 BC 的中点,点 P 在射线 AD 上,过点 P 作 PF⊥AE,垂足为 F. (1)、求证:△PFA∽△ABE;(2)、当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶点的三角形也与△ABE
(1)、求证:△PFA∽△ABE;(2)、当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶点的三角形也与△ABE相似?若存在,求出 x 的值;若不存在,说明理由.
22. “农民也能报销医疗费了!”这是国家推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款,这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.根据以上信息,解答以下问题:
 (1)、本次调查了名村民,被调查的村民中,有人参加合作医疗得到了返回款?
(1)、本次调查了名村民,被调查的村民中,有人参加合作医疗得到了返回款?
(2)、若该乡有10000名村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年平均增长率相同,求年平均增长率.
23. 当前,交通拥堵是城市管理的一大难题.我市城东高架桥的开通为分流过境车辆、缓解市内交通压力 起到了关键作用,但为了保证安全,高架桥上最高限速 80 千米/小时.在一般条件下,高架桥上的车流 速度 v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数,当桥上的车流密度达到 180 辆/千 米时,造成堵塞,此时车流速度为 0;当 0≤x≤20 时,桥上畅通无阻,车流速度都为 80 千米/小时, 研究表明:当 20≤x≤180 时,车流速度 v 是车流密度 x 的一次函数.
(1)、当 0≤x≤20 和 20≤x≤180 时,分别写出函数 v 关于 x 的函数关系式;
(2)、当车流密度 x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)w=x·v可以达到最大,并求出最大值;(3)、某天早高峰(7:30—9:30)经交警部门控制管理,桥上的车流速度始终保持 40 千米/小时,问这天 早高峰期间高架桥分流了多少辆车?
24.(1)、知识储备①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.

②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)、知识迁移①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段的长度即为△ABC 的费马距离.
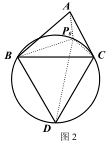
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
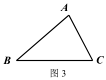 (3)、知识应用
(3)、知识应用①判断题:
ⅰ.任意三角形的费马点有且只有一个();
ⅱ.任意三角形的费马点一定在三角形的内部().
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为 ,求正方形 ABCD 的边长.
