浙江省绍兴市2018届九年级数学中考一模试卷

试卷更新日期：2018-08-10 类型：中考模拟

进入出卷网下载

一、单选题

1. 二次函数y=（x﹣1）²+2的最小值是（）

A、﹣2 B、2 C、﹣1 D、 1

查看试题解析
2. 已知⊙O的半径为5，若PO=4，则点P与⊙O的位置关系是（）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法判断

查看试题解析
3. 已知一个扇形的半径为R，圆心角为n°，当这个扇形的面积与一个直径为R的圆面积相等时，则这个扇形的圆心角n的度数是（）

A、180° B、120° C、90° D、60°

查看试题解析
4. 如图，点A，C，B在⊙O上，已知∠AOB=∠ACB= $α$ ，则 $α$ 的值为（）

A、135° B、100° C、110° D、120°

查看试题解析
5. 如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（）

A、 $\frac{1}{2}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{10}}{10}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
6. 小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸板的面积是（）

A、120πcm² B、240πcm² C、260πcm² D、480πcm²

查看试题解析
7. 二次函数y=ax²+bx+c（a≠0）的图象如图，下列结论：
①c＜0；②b＞0； ③4a+2b+c＞0； ④（a+c）²＜b² ．其中不正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，PA，PB分别切⊙O于A，B两点，射线PD与⊙O相交于C，D两点，点E是CD中点，若∠APB=40°，则∠AEP的度数是（）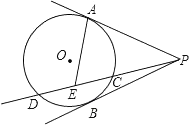

A、40° B、50° C、60° D、70°

查看试题解析
9. 利用平方根去根号可以构造一个整系数方程．例如：x= $\sqrt{2}$ +1时，移项得x﹣1= $\sqrt{2}$ ，两边平方得（x﹣1）²=（ $\sqrt{2}$ ）² ，所以x²﹣2x+1=2，即x²﹣2x﹣1=0．仿照上述构造方法，当x= $\frac{\sqrt{6} - 1}{2}$ 时，可以构造出一个整系数方程是（）

A、4x²+4x+5=0 B、4x²+4x﹣5=0 C、x²+x+1=0 D、x²+x﹣1=0

查看试题解析
10. 如图，AB是⊙O的直径，弦CD⊥AB于点G．点F是CD上一点，且满足 $\frac{C F}{F D} = \frac{1}{3}$ ，连接AF并延长交⊙O于点E．连接AD、DE，若CF=2，AF=3．给出下列结论：
①△ADF∽△AED；②FG=2；③tan∠E= $\frac{\sqrt{5}}{2}$ ；④S_△_DEF=4 $\sqrt{5}$ ．
其中正确的是（）

A、①②④ B、①②③ C、②③④ D、①③④

查看试题解析

二、填空题

11. 比较三角函数值的大小：sin30° tan30°（填入“＞”或“＜”）．

查看试题解析
12. 有9张卡片，每张卡片上分别写有不同的从1到9的一个自然数，从中任意抽出一张卡片，则抽到的卡片上的数是3的倍数的概率是

查看试题解析
13. 如图，在直角三角形ABC中（∠C=90°），放置边长分别3，4，x的三个正方形，则x的值为．

查看试题解析
14. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么PB的长度为 cm．

查看试题解析
15. 如图，已知在Rt△ABC中，∠C为直角，AC=5，BC=12，在Rt△ABC内从左往右叠放边长为1的正方形小纸片，第一层小纸片的一条边都在AB上，依次这样往上叠放上去，则最多能叠放个．

查看试题解析
16. 如图，在⊙O中，AB为⊙O的直径，AB=4．动点P从A点出发，以每秒π个单位的速度在⊙O上按顺时针方向运动一周．设动点P的运动时间为t秒，点C是圆周上一点，且∠AOC=40°，当t=秒时，点P与点C中心对称，且对称中心在直径AB上．

查看试题解析

三、解答题

17. 计算：

(1)、（﹣1）²+tan45°﹣ $\sqrt{4}$ ；

(2)、已知 $\frac{x}{y} = \frac{2}{3}$ ，求 $\frac{3 x - y}{x + 2 y}$ 的值．

查看试题解析
18. 动手画一画，请把如图补成以A为对称中心的中心对称图形．

查看试题解析
19. 甲口袋中装有两个相同的小球，它们的标号分别为2和7，乙口袋中装有两个相同的小球，它们的标号分别为4和5，丙口袋中装有三个相同的小球，它们的标号分别为3，8，9．从这3个口袋中各随机地取出1个小球．

(1)、求取出的3个小球的标号全是奇数的概率是多少？

(2)、以取出的三个小球的标号分别表示三条线段的长度，求这些线段能构成三角形的概率．

查看试题解析
20. 如图，在△ABC中，AC=8cm，BC=16cm，点P从点A出发，沿着AC边向点C以1cm/s的速度运动，点Q从点C出发，沿着CB边向点B以2cm/s的速度运动，如果P与Q同时出发，经过几秒△PQC和△ABC相似？

查看试题解析
21. 如图，阳光通过窗口照到教室内，竖直窗框在地面上留下2.1 m长的影子如图所示，已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m，窗口底边离地面的距离BC=1.2 m，试求窗口的高度（即AB的值）．

查看试题解析
22. 在△ABC中，∠CAB=90°，AD⊥BC于点D，点E为AB的中点，EC与AD交于点G，点F在BC上．

(1)、如图1，若AC：AB=1：2，EF⊥CB，求证：EF=CD；

(2)、如图2，若AC：AB=1： $\sqrt{3}$ ，EF⊥CE，求EF： EG的值.

查看试题解析
23. 阅读理解：如图1，在四边形ABCD的边AB上任取一点E（点E不与点A、点B重合），分别连接ED，EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的相似点；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的强相似点．
解决问题：

(1)、如图1，∠A=∠B=∠DEC=55°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；

(2)、如图2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD的边AB上的一个强相似点E；
拓展探究：

(3)、如图3，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB和BC的数量关系．

查看试题解析
24. 已知x轴上有点A（1，0），点B在y轴上，点C（m，0）为x轴上一动点且m＜﹣1，连接AB，BC，tan∠ABO= $\frac{1}{2}$ ，以线段BC为直径作⊙M交直线AB于点D，过点B作直线l∥AC，过A，B，C三点的抛物线为y=ax²+bx+c，直线l与抛物线和⊙M的另一个交点分别是E，F．

(1)、求B点坐标；

(2)、用含m的式子表示抛物线的对称轴；

(3)、线段EF的长是否为定值？如果是，求出EF的长；如果不是，说明理由．

(4)、是否存在点C（m，0），使得BD= $\frac{1}{2}$ AB？若存在，求出此时m的值；若不存在，说明理由．

查看试题解析