浙江省金华市2018届数学中考一模试卷

试卷更新日期：2018-08-10 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 3$ 的相反数是 $($ $)$

A、3 B、 $- 3$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下列调查中，适宜采用普查方式的是 $($ $)$

A、调查热播电视剧 $《$ 人民的名义 $》$ 的收视率 B、调查重庆市民对皮影表演艺术的喜爱程度 C、调查某社区居民对重庆万达文旅城的知晓率 D、调查我国首艘货运飞船“天舟一号”的零部件质量

查看试题解析
3. 本学期，大兴区开展了“恰同学少年，品诗词美韵”中华传统诗词大赛活动 $.$ 小江统计了班级30名同学四月份的诗词背诵数量，具体数据如表所示：
诗词数量 $($ 首 $)$
4
5
6
7
8
9
10
11
人数
3
4
4
5
7
5
1
1
那么这30名同学四月份诗词背诵数量的众数和中位数分别是（）

A、11，7 B、7，5 C、8，8 D、8，7

查看试题解析
4. 如图，四边形ABCD内接于 $⊙ O$ ，若四边形ABCO是平行四边形，则 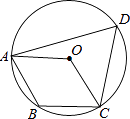$∠ A D C$ 的大小为（）

A、 $45^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $75^{\circ}$

查看试题解析
5. 已知直线 $m / / n$ ，将一块含 $30^{\circ}$ 角的直角三角板ABC按如图方式放置 $(∠ A B C = 30^{\circ})$ ，其中A，B两点分别落在直线m，n上，若 $∠ 1 = 20^{\circ}$ ，则 $∠ 2$ 的度数为（）

A、 $20^{\circ}$ B、 $30^{\circ}$ C、 $45^{\circ}$ D、 $50^{\circ}$

查看试题解析
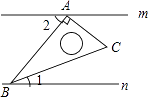6. 在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强，如下表：则可以反映y与x之间的关系的式子是（）
体积 x(mL) 100 80 60 40 20
压强 y(kPa) 60 75 100 150 300

A、 $y = 3$ 000x B、 $y = 6$ 000x C、 $y = \frac{3000}{x}$ D、 $y = \frac{6000}{x}$

查看试题解析
7. 如图，AB是半圆O的直径，点C在半圆O上，把半圆沿弦AC折叠， $\overset{⌢}{A C}$ 恰好经过点O，则 $\overset{⌢}{B C}$ 与 $\overset{⌢}{A C}$ 的关系是（）

A、 $\overset{⌢}{B C} = \frac{1}{2} \overset{⌢}{A C}$ B、 $\overset{⌢}{B C} = \frac{1}{3} \overset{⌢}{A C}$ C、 $\overset{⌢}{B C} = \overset{⌢}{A C}$ D、不能确定

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ C = 90^{\circ}$ ， $A C = 6$ ， $B C = 8.$ 在 $△ A B C$ 内并排 $($ 不重叠 $)$ 放入边长为1的小正方形纸片，第一层小纸片的一条边都在AB上，首尾两个正方形各有一个顶点分别在AC，BC上，依次这样摆放上去，则最多能摆放（）个小正方形纸片．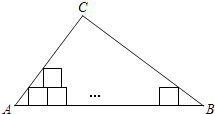

A、14个 B、15个 C、16个 D、17个

查看试题解析
9. 如图，在矩形ABCD中， $A B < B C$ ，E为CD边的中点，将 $△ A D E$ 绕点E顺时针旋转 $180^{\circ}$ ，点D的对应点为C，点A的对应点为F，过点E作 $M E ⊥ A F$ 交BC于点M，连接AM、BD交于点N，现有下列结论： $① A M = A D + M C$ ； $② A M = D E + B M$ ； $③ D E^{2} = A D \cdot C M$ ； $④$ 点N为 $△ A B M$ 的外心．其中正确的个数为（）

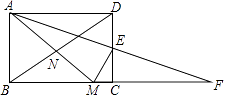A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

10. 二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
11. 分解因式： $x^{3} - 2 x^{2} y + x y^{2} =$ ．

查看试题解析
12. 将一个半径为6cm，母线长为15cm的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是度 $.$

查看试题解析
13. 小鹏早晨到校发现作业忘带，就打电话叫爸爸立即把作业送到学校，小鹏也同时往家赶，两人相遇后，小鹏以原速度返回学校，爸爸则以原速度的 $\frac{2}{3}$ 返回家 $.$ 设爸爸行走的时间为x分钟，小鹏和爸爸两人之间的距离为y米，y与x的函数关系如图所示，则当小鹏回到学校时，爸爸还需要分钟才能到家．

查看试题解析
14. 如图， $△ A B C$ 是边长为1的等边三角形 $.$ 取BC边中点E，作 $E D / / A B$ ， $E F / / A C$ ，得到四边形EDAF，它的面积记作 $S_{1}$ ；取BE中点 $E_{1}$ ，作 $E_{1} D_{1} / / F B$ ， $E_{1} F_{1} / / E F$ ，得到四边形 $E_{1} D_{1} F F_{1}$ ，它的面积记作 $S_{2} .$ 照此规律作下去，则 $S_{2011} =$ ．

查看试题解析
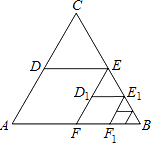15. 如图，点A是反比例函数 $y = \frac{k}{x} (k > 0)$ 图象第一象限上一点，过点A作 $A B ⊥ x$ 轴于B点，以AB为直径的圆恰好与y轴相切，交反比例函数图象于点C，在AB的左侧半圆上有一动点D，连结CD交AB于点 $E .$ 记 $△ B D E$ 的面积为 $S_{1}$ ， $△ A C E$ 的面积为 $S_{2}$ ，连接BC，则 $△ A C B$ 是三角形，若 $S_{1} - S_{2}$ 的值最大为1，则k的值为.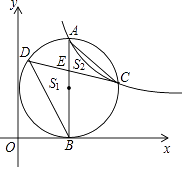

查看试题解析

三、解答题

16. 计算： $\sqrt{18} + | 2 \sqrt{2} - 8 | - {(\frac{1}{3})}^{- 1} - 2 \sqrt{3} cos 30^{\circ}$ ．

查看试题解析
17. 为更好地开展选修课，戏剧社的张老师统计了近五年该社团学生参加市级比赛的获奖情况，并绘制成如下两幅不完整的统计图，请根据图中的信息，完成下列问题：

(1)、该社团2017年获奖学生人数占近五年获奖总人数的百分比为，补全折线统计图；

(2)、该社团2017年获奖学生中，初一、初二年级各有一名学生，其余全是初三年级学生，张老师打算从2017年获奖学生中随机抽取两名学生参加学校的艺术节表演，请你用列表法或画树状图的方法，求出所抽取两名学生恰好都来自初三年级的概率．

查看试题解析
18. 某农机租赁公司共有50台收割机，其中甲型20台，乙型30台，现将这50台联合收割机派往A，B两地区收割水稻，其中30台派往 A地区，20台派往 B地区，两地区与该农机公司商定的每天租赁价格如表：

每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元

(1)、设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y元，求y关于x的函数关系式；

(2)、若使农机租赁公司这50台收割机一天所获租金不低于79600元，试写出满足条件的所有分派方案；

(3)、农机租赁公司拟出一个分派方案，使该公司50台收割机每天获得租金最高，并说明理由．

查看试题解析
19. 已知：如图一，抛物线 $y = a x^{2} + b x + c$ 与x轴正半轴交于A、B两点，与y轴交于点C，直线 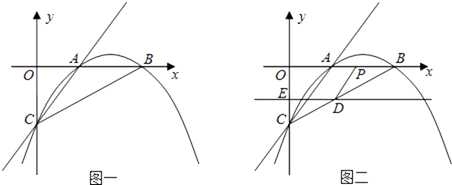$y = x - 2$ 经过A、C两点，且 $A B = 2$ ．

(1)、求抛物线的解析式；

(2)、若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动， $($ 如图 $2)$ ；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设 $s = \frac{E D + O P}{E D \cdot O P}$ ，当t为何值时，s有最小值，并求出最小值．

(3)、在 $(2)$ 的条件下，是否存在t的值，使以P、B、D为顶点的三角形与 $△ A B C$ 相似；若存在，求t的值；若不存在，请说明理由．

查看试题解析
20. 先化简，再求值： $\frac{x^{2} + 1}{x^{2} - 1} - \frac{x - 2}{x - 1} \div \frac{x - 2}{x}$ ，其中 $x = - 2$ ．

查看试题解析
21. 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．

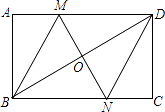(1)、求证：四边形BMDN是菱形；

(2)、若 $A B = 4$ ， $A D = 8$ ，求菱形BMDN的面积和对角线MN的长．

查看试题解析
22. 如图，已知反比例函数 $y = \frac{8}{x}$ 与一次函数 $y = k x + b$ 的图象交于A、B两点，且点A的横坐标是2，点B的纵坐标是 $- 2.$ 求：

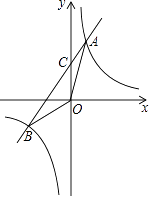(1)、一次函数的解析式；

(2)、 $△ A O B$ 的面积；

(3)、直接写出使反比例函数的值大于一次函数的值的x的取值范围．

查看试题解析
23. 阅读理解：如图，在平面直角坐标系xOy中，点A与点B的坐标分别是 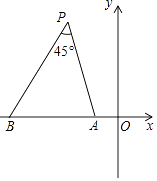$(- 1 ， 0)$ ， $(- 7 ， 0)$ ．

(1)、对于坐标平面内的一点P，给出如下定义：如果 $∠ A P B = 45^{\circ}$ ，则称点P为线段AB的“等角点” $.$ 显然，线段AB的“等角点”有无数个，且A、B、P三点共圆．
$①$ 设A、B、P三点所在圆的圆心为C，直接写出点C的坐标和 $⊙ C$ 的半径；
$② y$ 轴正半轴上是否有线段AB的“等角点”？如果有，求出“等角点”的坐标；如果没有，请说明理由；

(2)、当点P在y轴正半轴上运动时， $∠ A P B$ 是否有最大值？如果有，说明此时 $∠ A P B$ 最大的理由，并求出点P的坐标；如果没有请说明理由．

查看试题解析

	每台甲型收割机的租金	每台乙型收割机的租金
A地区	1800元	1600元
B地区	1600元	1200元

诗词数量 $($ 首 $)$	4	5	6	7	8	9	10	11
人数	3	4	4	5	7	5	1	1

体积 x(mL)	100	80	60	40	20
压强 y(kPa)	60	75	100	150	300